Kezdőlap


Feladat:	383. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Bakay B. , Barabási L. , Budó Á. , Busztin Anna , Csipkay Gy. , Deutsch E. és I. , Dux Klára , Erdélyi Erzsi , Ernst F. , Gál L. , Gerber Edit , Gerencsér I. , Gohn E. , Goldschmidt P. , Goldstein E. , Kaufmann I. , Klein B. , Klein M. , Klinger Lilly , Konoschek P. , Kozma M. , Lang L. , Lukács S. , Máté T. , Mitnyán L. , Molnár J. , Nánási Gy. , Névai L. , Paskusz Vera , Rusz Gy. , Scheibner K. , Székely I.
Füzet:	1929/január, 135 - 136. oldal		PDF \| MathML
Témakör(ök):	Körök, Gyakorlat
Hivatkozás(ok):	Feladatok: 1928/november: 383. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . a) Legyen $P$ pont a körön belül; húzzunk a $P$ ponton át átmérőt, melynek végpontjai legyenek $A$ és $B$ . Az $A$ legyen a messzebb fekvő, $B$ a közelebb fekvő. Ekkor $P B$ a legkisebb, $P A$ a legnagyobb távolsága a $P$ pontnak a kör pontjaitól.

Vegyük fel a körön az

M

pontot, a

B

közelében.

Az

O P M ▵

-ben

\begin{matrix} O M - O P < P M . \end{matrix}

O M = O B

; tehát

O M - O P = O B - O P = P B

. Eszerint

\begin{matrix} P B < P M . \end{matrix}

Vegyük fel most a körön az

N

pontot az

A

közelében. A

C P N ▵

-ben

\begin{matrix} O P + O N > P N . \end{matrix}

Azonban

O N = O A

; tehát

O P + O N = O P + O A = P A

. Így

P A > P N

.
b) Legyen

P

pont a körön kívül és a

P

-ből húzott átmérő végpontjai legyenek

A

és

B

, úgy mint előbb.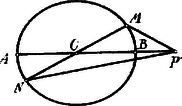

Most a

P O M ▵

-ben

\begin{matrix} P O < P M + O M . \end{matrix}

Azonban

\begin{matrix} P O = P B + B O, tehát P B + B O < P M + O M . \end{matrix}

Mivel

\begin{matrix} B O = O M, lesz: P B < P M \end{matrix}

azaz

P B

P

pont legkisebb távolsága a kör pontjaitól. Másrészt a

P O N ▵

-ben:

\begin{matrix} P O + O N > P N . \end{matrix}

Mivel

\begin{matrix} O N = O A, P O + O N = P O + O A = P A > P N . \end{matrix}

Ezek alapján kimondhatjuk, hogy a

P

pont legközelebb van a rajta átmenő átmérő közelebb fekvő végpontjához; a másik végpontjától pedig távolabb van, mint a kör bármely más pontjától.
Ha a

P

pont a körön van, legközelebb van önmagához, legtávolabb a diametrálisan szemben fekvő ponttól.

2^{\circ}

. A két kör feküdjék egymáson kívül, ne legyen közös pontjuk. Az

O_{1}

és

O_{2}

középpontokat összekötő egyenesen az átmérők:

A_{1} B_{1}

, ill.

A_{2} B_{2}

, mégpedig úgy, hogy az

A_{1}

és

A_{2}

végpontok belül feküsznek. Kimutatjuk, hogy a két kör pontjai között

\begin{matrix} A_{1} A_{2} a legrövidebb, B_{1} B_{2} a leghosszabb távolság. \end{matrix}

a) Az

O_{1}

körön vegyük fel az

M_{1}

, az

O_{2}

körön az

M_{2}

pontot. Az

M_{1} M_{2}

távolságnál kisebbet kapunk az

1^{\circ}

. a) szerint, ha pl. az

M_{1}

pontot összekötve az

O_{2}

középponttal, az így keletkező átmérőnek

M_{1}

-hez közelebb fekvő végpontját vesszük, azaz: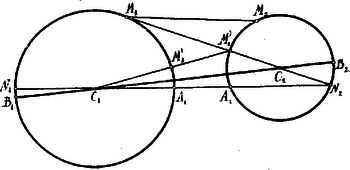

M_{1} M'_{2} < M_{1} M_{2}

Most az

M'_{2}

-t kötjük össze az

O_{1}

ponttal:

M'_{2} M'_{1} < M_{1} M'_{2}

s. í. t. eljárva mindig kisebbet kapunk. Ha azonban az

O_{1} O_{2}

centrálison fekvő

A_{1} A_{2}

távolságot tekintjük, ennél kisebbet nem kapunk.
b) Ha az

M_{1} O_{2}

egyenesen fekvő átmérő másik végpontját,

N_{2}

-t vesszük, akkor

1^{\circ}

. b) szerint:

M_{1} N_{2} > M_{1} M_{2}

. Az

N_{2} O_{1}

egyenesen fekvő átmérő

N_{1}

végpontjával:

N_{2} N_{1} > M_{1} N_{2}

, s. í. t. eljárva mindig nagyobb távolságokat kapunk; a

B_{1} B_{2}

távolságnál nagyobbat nem kapunk.
Hasonló gondolatmenetet követve állapíthatjuk meg két kör pontjai között a legkisebb és legnagyobb távolságot, a körök egyéb helyzetei mellett.

Gerber Edit (izr. leánygimn. VI. o. Bp.)

Jegyzet. A felsoroltakon kívül beérkezett még 20 megoldás, amelyekben az állítás nincs bizonyítva.