Kezdőlap


Feladat:	340. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aschenbrier E. , Bakay B. , Barok Gy. , Bauer J. , Beke I. , Bolgár Gy. , Buzna V. , Csiky J. , Hapka I. , Kiss Gy. , Liebermann J. , Ligeti Miklós , Lukács S. , Magyarka F. , Radó Gy. , Sebők Gy. , Simon Á. , Soos G. , Stern M. , Straubert F. , Vági L.
Füzet:	1928/szeptember, 10 - 11. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1928/április: 340. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a négyszög szögei $α$ , $β$ , $γ$ , $δ$ és tegyük fel, hogy $A'$ és $C$ a $C D$ ill. $A B$ oldalakon (tehát nem meghosszabbításukon) feküsznek. Ekkor a $B C C' ▵$ -ből a $C'$ -nél lévő külső szög: $\hat{C C' A} = \hat{B} + \hat{B C C'} = β + \frac{γ}{2}$ ; ugyanígy $\hat{A A' C} = \hat{D} + \hat{D A A'} = δ + \frac{α}{2}$ , vagy, mivel feltevés szerint $β = δ$ , $\hat{A A' C} = β + \frac{α}{2}$ ; továbbá az $A C' C A'$ négyszögben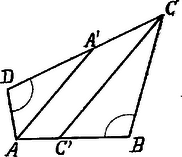

\begin{matrix} \hat{A} = \frac{α}{2}, \hat{C} = \frac{γ}{2}, tehát \hat{A} + \hat{C'} = \hat{A'} \hat{C} = β + \frac{α}{2} + \frac{γ}{2} . \end{matrix}

De ekkor az

A C' C A'

idom trapéz, melynek párhuzamos oldalai

A A'

és

C C'

Ez, mivel oldalai ismeretesek, szerkeszthető (a párhuzamos oldalak különbségével és a másik két oldallal háromszöget szerkesztünk, stb). Ezután megszerkesztjük az

A C'

-vel

A A'

-re és

C A'

-vel

C C'

-re vonatkozólag szimmetrikus egyeneseket; az első

C A'

-t

D

-ben, a második

A C'

-t

B

-ben metszi.
Ha az

A'

és

C'

C D

és

A B

oldalak meghosszabbítására esnek, az

A C' C A'

négyszög minden szöge az előbbi szögek mellékszöge lesz; a többi megállapítás és a szerkesztés menete teljesen ugyanaz.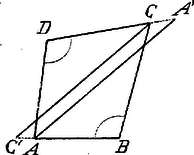

Ligeti Miklós (Baross Gábor főrál VI. o. Szeged.)

Jegyzet. Ha

A A' > C C'

és

A C' > C A'

vagy megfordítva egyszerre fennállanak, akkor

A'

és

C'

az oldalakra esnek; meghosszabbításaikra, ha pl.

A A' > C C'

A C' < C A'