Kezdőlap


Feladat:	337. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bauer József , Erhardt Gy. , Feldheim E. , Fürst H. , Gál L. , Hapka I. , Holczinger I. , Kiss Gy. , Liebermann J. , Ligeti M. , Papp Gy. , Simon Á. , Soos G. , Stern M. , Straubert J. , Székely I. , Vági L.
Füzet:	1928/szeptember, 8 - 9. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1928/április: 337. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a gummifonál azon pontjai, melyekkel az éppen ráfekszik a körök kerületeire rendre: 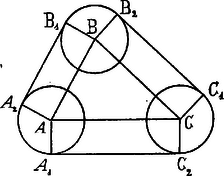$A_{1}$ , $A_{2}$ , $B_{1}$ , $B_{2}$ , $C_{1}$ , $C_{2}$ .

A fonál hossza:

k = (\bar{A_{2} B_{1}} + \bar{B_{2} C_{1}} + \bar{C_{2} A_{1}}) + (\hat{A_{1} A_{2}} + \hat{B_{1} B_{2}} + \hat{C_{1} C_{2}}) = e + i

; egyenes részei a 3 kör közül 2‐2-t érintenek, de a körök sugarai egyenlők, tehát

A B B_{1} A_{2}

B C C_{1} B_{2}

C A A_{1} C_{2}

idomok parallelogrammák s így

A_{2} B_{1} = A B

B_{2} C_{1} = B C

C_{2} A_{1} = C A

e = 2 s =

A B C

háromszög kerülete.
Legyen

\hat{A_{1} A A_{2}} = α_{1}

\hat{B_{1} B B_{2}} = β_{1}

\hat{C_{1} C C_{2}} = γ_{1}

(fokokban); ekkor

\begin{matrix} \hat{A_{1} A_{2}} = \frac{r π α_{1}}{180^{\circ}}, \hat{B_{1} B_{2}} = \frac{r π β_{1}}{180^{\circ}}, \hat{C_{1} C_{2}} = \frac{r π γ_{1}}{180^{\circ}} \end{matrix}

és így

\begin{matrix} i = \frac{r π (α_{1} + β_{1} + γ_{1})}{180^{\circ}} . \end{matrix}

Azonban

α_{1} = 360^{\circ} - A \hat{A_{2} A B} - \hat{B A C} - \hat{C A A_{1}} = 360^{\circ} - α - 90^{\circ} = 180^{\circ} - α

, hol

α

A B C

háromszög szöge, ugyanígy

β_{1} = 180^{\circ} - β

γ_{1} = 180^{\circ} - γ

, tehát

\begin{matrix} α_{1} + β_{1} + γ_{1} = 360^{\circ} és i = 2 r π; \end{matrix}

a gummifonál hossza tehát

k = e + i = 2 s + 2 r π

.
A fonállal bezárt terület:

\begin{matrix} T & = A B C + A B B_{1} A_{2} + B C C_{1} B_{2} + C A A_{1} C_{2} + A_{1} A A_{2} + B_{1} B B_{2} + C_{1} C C_{2} = \\ = t + A B \cdot r + B C \cdot r + C A \cdot r + \frac{r^{2} π α_{1}}{360^{\circ}} + \frac{r^{2} π β_{1}}{360^{\circ}} + \frac{r^{2} π γ_{1}}{360^{\circ}} \\ T & = t + (A B + B C + C A) r + \frac{r^{2} π}{360^{\circ}} + (α_{1} + β_{1} + γ_{1}) \\ T & = t + 2 s r + r^{2} π . \end{matrix}

Ha az

n

kör egymáson kivül fekszik és az

A_{1}

...

A_{n}

középpontok állal meghatározott sokszög minden szöge kisebb

180^{\circ}

-nál (azaz a sokszög konvex), e sokszög kerülete

2 s

és területe

t

, akkor a fonál hossza:

k = 2 s + 2 r π

, a bezárt terület pedig

T = t + 2 s r + r^{2} π

. Ugyanis az egyenes fonalrészekre és az egyenes vonalakkal határolt területrészletekre fennállanak előbbi megállapításaink, ha pedig az előbbi

_{1}

indexes szögeket

'

-vel jelöljük

α'_{1} = 180^{\circ} - α_{1}

...

α'_{n} = 180^{\circ} - α_{n}

és így

α'_{1} + ... + α'_{n} = n \cdot 180^{\circ} - (α_{1} + ... + α_{n})

, hol

α_{1}

...

α_{n}

a középpontok sokszögének szögei és így

α_{1} + ... + α_{n} = (n - 2) 180^{\circ}

, tehát

α'_{1} + ... + α'_{n} = 360^{\circ}

, ugyanúgy mint háromszög esetén.

Bauer József (Szent-László rg. V. o. Bp. X.)