Kezdőlap


Feladat:	316. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Antal Aladár , Bakay B. , Barna I. , Barok Gy. , Bauer József , Beke I. , Bolgár Gy. , Buzna V. , Csiky J. , Dobó M. , Dvorzsák Zs. , Erhardt Gy. , Feldheim E. , Fenyő L. , Goldfinger Gy. , Grosz E. , Grünwald T. , Hapka I. , Holczinger I. , Katz Z. , Klein Imre (Debrecen) , Klein István , Krausz Erzsébet , Lichtenstein S. , Ligeti M. , Lőw A. , Papp Gy. , Pomóthy D. , Radó Gy. , Rasovszky E. , Sámuel J. , Simon Á. , Soos Géza , Stern M. , Szalai Sándor , Széll J. , Török I. , Zsendovics E.
Füzet:	1928/április, 232 - 233. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Alakzatba írt kör, Derékszögű háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1928/február: 316. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az érintő kör középpontja $I$ az $A O B ∢$ -et felező $O M$ egyenesen fekszik. Az $A B$ ív $M$ felezőpontjában állítsunk $O M$ -re merőlegest, mely $O A$ -t $K$ $O B$ -t $L$ pontban metszi, továbbá az $I$ pontból $O A$ -ra, melynek talppontja 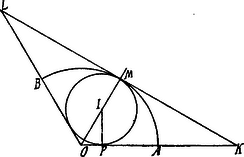$P$ .

Ekkor

\begin{matrix} O I P ▵ \sim O K M ▵; \end{matrix}

mind a kettő mintaháromszög. Eszerint

\begin{matrix} O I : I P = O K : M K . \end{matrix}

Legyen most már

O A = O B = O M = R

;

I M = I P = ϱ

. Az

O M K

mintaháromszögben

\begin{matrix} O K = 2 O M = 2 R; M K = O M \sqrt[]{3} = R \sqrt[]{3}; \end{matrix}

továbbá

O I = O M - I M = R - ϱ

. Így

\begin{matrix} R - ϱ : ϱ = 2 R : R \sqrt[]{3} vagy R : p = 2 + \sqrt[]{3} : \sqrt[]{3} \\ ϱ = \frac{R \sqrt[]{3}}{2 + \sqrt[]{3}} = R \sqrt[]{3} (2 - \sqrt[]{3}) = R (2 \sqrt[]{3} - 3) . \end{matrix}

Bauer József (Szent László rg. V. o. Bp. X.)

Jegyzet. Van azonban oly kör is, mely az

A B

körívet kívülről érinti; ha ennek sugara

ϱ'

, akkor

\begin{matrix} R + ϱ' : ϱ' = 2 R : R \sqrt[]{3}, vagy R : ϱ' = 2 - \sqrt[]{3} : \sqrt[]{3} \\ ϱ' = \frac{R \sqrt[]{3}}{2 - \sqrt[]{3}} = R (2 \sqrt[]{3} + 3) . \end{matrix}

II. Megoldás. Alkalmazzuk az

O I P ▵

-re Pythagoras tételét;

O I = R - ϱ

\begin{matrix} O P = \frac{R - ϱ}{2}, I P = ϱ; tehát \\ {(\frac{R - ϱ}{2})}^{2} + ϱ^{2} = {(R - ϱ)}^{2} rendezve: ϱ^{2} + 6 R ϱ - 3 R^{2} = 0. \end{matrix}

Ezen egyenletnek van egy poz. és egy neg. gyöke; a viszonyoknak az előbbi felel meg. Ennek értéke:

\begin{matrix} ϱ = \frac{- 6 R + \sqrt[]{36 R^{2} + 12 R^{2}}}{2} = R (2 \sqrt[]{3} - 3) . \end{matrix}

Antal Aladár (Dobó István főreál V. o. Eger)

Jegyzet. Ha az egyenlet negatív gyökét ellenkező előjellel vesszük, megkapjuk a másik érintő körsugarát

(ϱ')

. Erre nézve ugyanis

\begin{matrix} {(\frac{R + ϱ'}{2})}^{2} + ϱ'^{2} = {(R + ϱ')}^{2} . \end{matrix}