Kezdőlap


Feladat:	293. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Bálint B. , Barabási L. , Barok György , Bauer J. , Dvorzsák Zs. , Erdős Pál , Feldheim E. , Fürst H. , Gerencsér I. , Gibolya T. , Klein Imre (Bp.) , Klein István , Kmoschek P. , Kovács T. , Láng S. , Liebermann J. , Molnár J. , Papp Gy. , Rasovszky E. , Salkovits E. , Sámuel J. , Selymes L. , Sólyom T. , Somló T. , Soos Géza , Stern M. , Szalai Sándor
Füzet:	1928/február, 174. oldal		PDF \| MathML
Témakör(ök):	Egyenletek grafikus megoldása, Fizikai jellegű feladatok, Együttes munkára vonatkozó feladatok, Folyadékok és gázok áramlása, Geometriai szerkesztések alkalmazása, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/december: 293. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az abcissa-tengelyre mért egységek jelentsék az időt (1 óra $= 1 cm.),$ az ordinátára pedig rakjuk a medence víztartalmát (az egész medence térfogata $ν = 2 cm.)$ ¹ Ha $I$ , $I I$ , $I I I$ rendre a $(3, ν),$ $(4, ν)$ , $(5, ν)$ pontokat jelölik, akkor az $O I$ , $O I I$ , $O I I I$ egyenesek pontjainak ordinátái az idő függvénye gyanánt tüntetik fel a medence víztartalmát, melyet az $1.$ , $2.$ , $3.$ csövek (külön-külön) szolgáltatnak.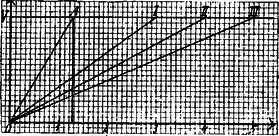

Hogyan változik a medence víztartalma, ha mind a három csapot egyszerre kinyitjuk? Ezt is egy egyenes pontjaihoz tartozó ordináták fogják feltüntetni. Hogy ezen egyenest megrajzolhassuk, elegendő két pontját ismernünk. Az egyik az

O

pont. A másikat megkapjuk, ha összeadjuk az

O I

O I I

O I I I

egyenesek egy bizonyos ‐ pl. az

x = 1

‐ abscissához tartozó pontjainak ordinátáit és ezt a távolságot az

x = 1

abscissa végpontjában felmérjük; ennek végpontja a keresett egyenes másik pontja. Ennek (t. i.

O A

) és a

ν = 1

egyenesnek metszéspontjához tartozó abscissa ‐ kb.

1, 27

‐ adja a medence megtöltéséhez szükséges időt. (A felmért ordináta:

\begin{matrix} \frac{1}{3} + \frac{1}{4} + \frac{1}{5} = \frac{47}{60} \end{matrix}

s így a metszéspont

x

abscissája

x : 1 = 1 : \frac{47}{60}

arányból

x = \frac{60}{47} \approx 1, 27)

Borok György (Koháry István rg. V. o. Gyöngyös.)

¹Így az ordináta egysége kétszerese az abscissáénak.