Kezdőlap


Feladat:	265. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Erdős Pál , Freytag A. , Grosz Endre , Salkovits E. , Soos Géza , Szikszay L. , Valkó Iván
Füzet:	1927/november, 76 - 77. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Paralelogrammák, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/szeptember: 265. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $O_{1} O_{2}$ centrális $C$ középpontját kössük össze az $A$ ponttal és $C A$ -ra emeljünk az $A$ pontban merőlegest; ezen merőleges a köröket a kivánt $M$ , ill. $N$ pontban metszi.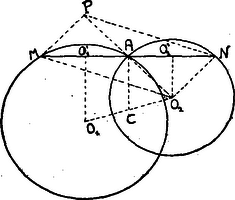

Ha ugyanis az

O_{1}

-ből

A M

-re,

O_{2}

-ből

A N

-re merőlegeseket állítunk és ezek talppontjai

O'_{1}

ill.

O'_{2}

, akkor

O_{1} O_{2} O'_{1} O'_{2}

idom trapéz, melynek

C A

középvonala felezi

O'_{1} O'_{2}

oldalt, tehát

O'_{1} A = A O'_{2}

és így

A M = 2 O'_{1} A = 2 A O'_{2} = A N

Grosz Endre (áll. Dobó István főreál V. o. Eger)

II. Megoldás. Tekintsük a feladatot megoldottnak. Kössük össze pl. az

O_{2}

középpontot

A

-val és

O_{2} A

-t hosszabbítsuk meg önmagával úgy, hogy

A P = O_{2} A

. Akkor az

O_{2} N P M

idomban az átlók

A

-ban felezik egymást, tehát parallelogrammával van dolgunk:

P M = O_{2} N = O_{2} A

.
Ha tehát a

P

pontból az

O_{2} A

sugárral kört rajzolunk, ez az

O_{1}

középpontú kört ‐ az A ponton kívül még ‐

M

pontban metszi.

A M

O_{2}

kört most már

N

pontban metszi úgy, hogy

A N = A M

. Ugyanis

A P M ▵ ≅ A O_{2} N ▵

mert mind a kettő egyenlőszárú háromszög, amelyeknek szárai és szögei egyenlők, tehát alapjuk is, t. i.

A M

és

A N

is egyenlő egymással. A két kör, melynek középpontja

O_{2}

ill.

P

és sugaruk egyenlő, t. i.

P A = O_{2} A

A

pontra nézve szimmetrikus helyzetű, tehát

A

pont ezen két kör mindegyik szelőjét, mely

A

ponton keresztül megy, felezi.

Szerk.