Kezdőlap


Feladat:	263. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dvorzsák Zs. , Erdős P. , Faragó L. , Freytag A. , Holczinger I. , Radó György , Salkovits E. , Soos G. , Szalai Sándor , Takács T. , Zöld J.
Füzet:	1927/november, 75 - 76. oldal		PDF \| MathML
Témakör(ök):	Egyenes, Mértani helyek, Síkbeli szimmetrikus alakzatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/szeptember: 263. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Legyen $M$ pont vetülete $M_{1}$ , $N$ ponté $N_{1}$ . Az $M_{1}$ pont felezi $A P$ -t, $N_{1}$ pedig $P B$ -t. Tehát $M N$ vetülete

\begin{matrix} M_{1} N_{1} = M_{1} P + P N_{1} = \frac{A P}{2} + \frac{P B}{2} = \frac{A B}{2} = \frac{d}{2} azaz constans. \end{matrix}

2^{\circ}

M M_{1}

A P M

egyenlőoldalú háromszög magasságvonala,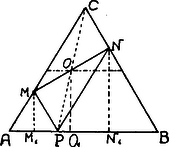

N N_{1}

P B N ▵

-é; tehát

\begin{matrix} M M_{1} = A P \frac{\sqrt[]{3}}{2} és N N_{1} = P B \frac{\sqrt[]{3}}{2} . \end{matrix}

M N

felezőponlja

O

, ennek vetülete

A B

-n

O_{1}

; de

O O_{1}

M M_{1} N N_{1}

trapéz középvonala és így

\begin{matrix} O O_{1} = \frac{M M_{1} + N N_{1}}{2} = \frac{1}{2} (A P + P B) \frac{\sqrt[]{3}}{2} = \frac{A B \sqrt[]{3}}{4} \end{matrix}

azaz

O

pont távolsága

A B

-től állandóan ugyanakkora, t. i. az

A B = d

oldalú szabályos háromszög magasságának fele. Eszerint

O

pont mértani helye az

A B

-vel párhuzamos vonaldarab, melynek távolsága

A B

-től

\frac{d \sqrt[]{3}}{4}

és határoló pontjai az

A B

fölött rajzolt egyenlő oldalú háromszög oldalainak (

A C

és

B C

) felezőpontjai.

Radó György (kegyesrendi g. VI. o. Bp.)

I. Jegyzet. Kössük össze az

A B C

egyenlő oldalú háromszög

C

csúcsát a

P

ponttal. Minthogy

C M P N

idom parallelogramma, ennek

C P

átlója felezi az

M N

átlót, azaz

M N

felezőpontja

O

C P

-nek is felezőpontja.

C P

felezőpontja, ha

P

végigfut az

A B

-n, az

A B

-vel párhuzamos vonaldarabot írja le, mely felezi

A C

-t és

B C

-t.
Jegyzet. Egyes megoldásokban a következő gondolatmenet nyilvánul: a mértani hely 3 pontja ‐ speciális helyzetben ‐ egy egyenesbe esik, tehát ezen mértani hely csak egyenes vonal lehet. Így nem szabad következtetnünk, mert elképzelhetünk görbe vonalat, melynek valamely egyenessel 3 közös pontja lehet. Azt lehetett volna mondani, hogy ezen vonal nem lehet kör (sem ellipszis, sem hiperbola, sem parabola).