Kezdőlap


Feladat:	239. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Camhi S. , Gelberger P. , Hajós György , Párducz N. , Sréter Jenő
Füzet:	1927/szeptember, 7 - 8. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Magasságvonal, Körülírt kör, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/április: 239. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $M M'$ érintő érintési pontja $P$ , $\bar{O' M'}$ felezőpontja $N$ , az $(O)$ és $(O')$ körök sugarai pedig 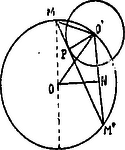$R$ és $r$ .

\hat{O' M P} \equiv \hat{O' M M'}

O

kör kerületi szöge, mely az

O' M'

ívhez tartozik és így fele az

\hat{O' O M'}

középponti szögnek, azaz

\hat{O' M P} = \hat{O' O N}

; ennélfogva

O' M P

és

O' O N

derékszögű háromszögek hasonlóak:

\begin{matrix} \bar{O' O} : \bar{O' N} = \bar{O' M} : \bar{O' P}, azaz R : \frac{\bar{O' M'}}{2} = \bar{O' M} : r, \end{matrix}

ahonnan

\begin{matrix} O' M \cdot O' M' = 2 R r = állandó. \end{matrix}

Sréter Jenő (izr. rg. VI. o. Debrecen)

Jegyzet. A tétel bizonyításánál hivatkozhatunk még arra, hogy az

O

kör az

O' M M' ▵

köré írt kör és ennek sugara

R = \frac{a b}{2 m}

vagyis

a b = 2 R m

, ahol

a

és

b

a háromszög két oldala ‐

O' M

és

O' M'

‐ és

m

a harmadik oldalra ‐

M M'

-re ‐ bocsátott magasság, a jelen esetben

O' P = r