Kezdőlap


Feladat:	217. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Ágoston A. , Blahó T. , Cambi S. , Hajós Gy. , Händler Gy. , Klein T. , Kőszeghy G. , Lőrincz Zsuzsi , Nádor L. , Pajzs T. , Párducz N. , Polacsek E. , Sebess B. , Soós Géza , Sréter J. , Sturm V. , Székely Lilly , Szolovits D. , Waldapfel L. , Walient P.
Füzet:	1927/április, 238. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Párhuzamos szelők tétele, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/február: 217. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ} .$ Legyen a trapéz $A B C D,$ a párhuzamos oldalak felezőpontjai $M$ és $N,$ a nem párhuzamos oldalak metszése pedig 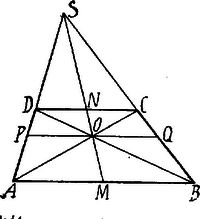$S .$

A B O ▵ \sim C D O ▵,

mert szögeik egyenlők, tehát

\begin{matrix} \bar{A O} : \bar{A B} = \bar{C O} : \bar{C D} . \end{matrix}

(1)

M

és

N

definiciója szerint

\bar{A B} = 2 \cdot \bar{A M}

és

\bar{C D} = 2 \cdot \bar{C N};

ezeket (1)-be helyettesítve, egyszerüsítés után kapjuk:

\begin{matrix} \bar{A O} : \bar{A M} = \bar{C O} : \bar{C N} . \end{matrix}

(2)

De ekkor

A M O ▵ \sim C N O ▵,

mert (2) szerint két oldaluk aránya egyenlő és az ezek által bezárt szögek is egyenlők:

M A O ∢ = N C O ∢,

tehát

M O A ∢ = N O C ∢ .

Eszerint

M O

és

N O

ugyanazon egyenest jelentik,

M

O

és

N

egy egyenesen vannak.
Ugyanígy

A B S ▵ \sim D C S ▵,

mert szögeik egyenlők, tehát

\begin{matrix} \bar{S A} : \bar{S D} = \bar{A B} : \bar{D C} = 2 \cdot \bar{A M} : 2 \cdot \bar{D N} = \bar{A M} : \bar{D N} . \end{matrix}

(3)

S D N ∢ = S A M ∢

s így (3) alapján,

S A M ▵ \sim S O N ▵,

miből

A S M ∢ = D S N ∢,

tehát

S M

és

S N

azonos egyenesek,

S

N

O

M

egy egyenesen vannak.

2^{\circ} .

S A

S M

S B

sugarakat az

A B | | P Q

egyenesekkel metszettük (a metszéspontok

A, M, B

ill.

P

O

Q

), tehát

\begin{matrix} \bar{P O} : \bar{O Q} = \bar{A M} : \bar{M B} = 1 : 1 s így \\ \bar{P O} = \bar{O Q} . \end{matrix}

Soós Géza (Szent-László rg. V. o. Bp. X.)