Kezdőlap


Feladat:	216. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ágoston E. , Beke István , Boschán Anna , Fürst H. , Gelberger P. , Grünwald Gy. , Győri János , Hajós Gy. , Jacobi A. , Juvancz I. , Katona J. , Kozma F. , Palatinus I. , Polacsek E. , Sréter J. , Sturm V. , Szolovits D. , Walient P. , Zwirn Gy.
Füzet:	1927/április, 236 - 237. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/február: 216. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Tekintsük a feladatot megoldottnak; legyen az adott háromszög $A B C,$ a beírt pedig $α β γ$ ( $α$ a $B C$ oldalon s. í t.).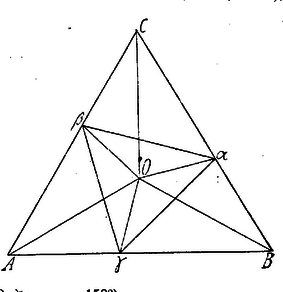

\begin{matrix} B α γ Δ - ből és B α C ∢ = 180^{\circ} - ból \\ α γ B ∢ = 180^{\circ} - B ∢ - B α γ ∢ = 120^{\circ} - B α γ ∢ \end{matrix}

és

\begin{matrix} β α C ∢ = 180^{\circ} - B α β ∢ - γ α β ∢ = 120^{\circ} - β α γ ∢ \end{matrix}

tehát

α γ B ∢ = β α C ∢;

ugyanígy

β α C ∢ = γ β A ∢ .

Minthogy továbbá

A ∢ = B ∢ = C ∢

és

\bar{α β} = \bar{β γ} = \bar{γ α},

A B C ▵

-ből az

α β γ

által levágott

α γ B, ...

háromszögek egybevágók s így

\bar{A γ} = \bar{B α} = \bar{C β} .

Ugyanez akkor is kimutatható, ha

α ...

csúcs a

B C, ...

oldal meghosszabbításán fekszik.
Kössük össze az

A, ...

és

α, ...

pontokat az

A B C ▵

köré írt kör

O

középpontjával. Így az

A γ O ▵ ≅ B α O ▵ ≅ C β O ▵,

minthogy bennük két-két oldal (

A γ, ...

és

A O, ...

) s az általuk bezárt szög (

γ A O ∢ = ... = 30^{\circ}

) egyenlők ‐ tehát

γ O = β O = α O,

s így

O

egyszersmind az

α β γ ▵

köré írt körnek is középpontja. (Ugyanez áll akkor is, ha

α

B C

oldal meghosszabbításán fekszik, csak akkor

γ A O ∢ = ... = 150^{\circ}

).
Ha megvan adva az

α β

oldal,

α O

sugár szerkesztéssel meghatározható.
Ezen az alapon most már a szerkesztés a következő: Az

A B C ▵

köré írt kör

O

középpontja mint középpont köré

α O

‐ adott sugarú kört írunk, ennek az

A B C ▵

oldalaival való metszéspontjai lesznek a keresett háromszög csúcsai.
Ennek a körnek az adott háromszög egy oldalával 2, 1, 0 közös pontja van. Ha a metszéspontok száma 2, két megoldást kapunk, de ezek lényegileg azonosak; egy közös pont esetén (

=

érintés) a közös pont az illető oldal felezőpontja,

α β γ ▵

oldalai ekkor

A B C

oldalainak félhosszai. Ha pedig közös pont nincs, megoldás sincs; ez akkor következik be, ha a beírandó háromszög oldala az adott felénél kisebb.

Győri János (Fáy András rg. VI. o. Bp. IX.)

II. Megoldás. Láttuk az I. megoldásban, hogy

\bar{A γ} = \bar{B α}

tehát

\begin{matrix} \bar{γ B} + \bar{B α} = \bar{A γ} + \bar{γ B} = A B . \end{matrix}

Eszerint

α β γ

háromszögben adva az

α γ

oldal, a másik két oldal összege

\bar{A B}

és a

B ∢ = 60^{\circ},

tehát e háromszög megszerkeszthető. A

\bar{γ δ} = \bar{A B}

távolság

δ

végpontjában

α δ γ = 30^{\circ}

-os szöget szerkesztünk, s ennek

δ α

szárát

\bar{γ δ} =

adott távolsággal elvágjuk.

α δ

felező merőlegese

γ δ

-t

B

-ben metszi. Itt

\bar{α B} = \bar{δ B}

és

α B γ ∢ = α δ γ ∢ + δ α B ∢ = 2 \cdot 30^{\circ} = 60^{\circ}

tehát a követelményeknek megfelel. A

B A

és

B C

egyenesek iránya így adott, s így

A B C ▵

is szerkeszthető.

Beke István (Toldi Ferenc főreál V. o. Bp. II.)