Kezdőlap


Feladat:	206. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Blahó T. , Bud Pál , Hajós Gy. , Rajz M. , Sréter J. , Szolovits Dezső
Füzet:	1927/március, 207 - 208. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1927/január: 206. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. $1^{\circ}$ . Legyenek az osztópontok $C$ és $D$ . $A C O ▵$ és $D B O ▵$ alkotórészei egymással egyenlők, mert 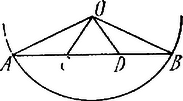$A C = D B$ , $A O = B O$ és $C A O ∢ = D B O ∢$ , tehát $A O C ∢ = D O B ∢$ .

Vizsgálnunk kell még a

C O D ∢

-et.

A D O ▵

-ben

O A = O D

; tudjuk azonban a 153. gyakorlatból (2. sz. 43. o.), hogy az

O C

oldalfelező a nagyobb oldallal zár be kisebb szöget, tehát

A O C ∢ < C O D ∢

: a szög középső része nagyobb a szélsőknél!

2^{\circ}

. Az

A B

ívet három egyenlő részre osztó pontok legyenek

C

és

D

C O

és

D O

sugarak pedig messék

\bar{A B}

-t

C_{1}

D_{1}

pontokban.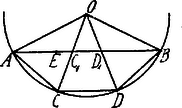

A C_{1} O

és

D_{1} B O

háromszögek alkotórészei ismét egyenlők, mert

A O = B O

A O C_{1} ∢ = B O D_{1} ∢

és

O A B ∢ = O B A ∢

, tehát

A C_{1} = B D_{1}

. Azonban

O C_{1}

A O D_{1} ∢

felezője és így a már említett 153. gyakorlat szerint, ha

E

A D_{1}

oldal felezőpontja,

D_{1} E = A E < A C_{1}

, tehát

C_{1} D_{1} < D_{1} E < A C_{1}

: a középső része a húrnak kisebb a szélsőknél!

Szolovits Dezső (izr. rg. VI. o. Debrecen)

II. Megoldás. Induljunk ki a

2^{\circ}

. esetből. Az

A B

ív osztópontjai legyenek

C

D

, a húréi pedig

C_{1}

D_{1}

.
A felosztás alapján

C D ∥ A B

\bar{A C} = \bar{C D}

és

A C O ∢ = O C D ∢

. Eszerint

\begin{matrix} A C O ∢ = O C D ∢ = O C_{1} D_{1} ∢ = A C_{1} C ∢, \end{matrix}

azaz

A C C_{1} ▵

egyenlőszárú, tehát

A C_{1} = A C

. Azonban

\begin{matrix} \bar{C_{1} D_{1}} < \bar{C D} = \bar{A C} = \bar{A C_{1}} = \bar{D_{1} B}; \end{matrix}

tehát a húr középső része kisebb a szélsőknél.

1^{0}

. Az eddigiekből kitűnik, hogy a középső szög csak akkor lehet egyenlő a külsőkkel, ha a hozzá tartozó húrmetszet kisebb a másik két húrmetszetnél. Ha tehát mindhárom, húrmetszet egyenlő, akkor a középső szögnek nagyobbnak kell lennie.

Bud Pál (kegyesrendi gimn. VI. o. Bp.)