Kezdőlap


Feladat:	126. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bandler Á. , Bányász István , Csalán E. , Hajós Gy. , Kecskeméti L. , Krausz Ilona , Lakatos L. , László B. , Scheiber P. , Schächter I. , Selymes L. (IV. o.) , Sveiczer M. , Szabó Ilona , Takács Lajos , Wachsberger Márta
Füzet:	1926/május, 267 - 268. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Síkgeometriai számítások trigonometria nélkül sokszögekben, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1926/március: 126. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Hogy a $P Q R ...$ sokszög szabályos nyolcszög, abból következik, hogy $A A_{1} P ▵$ és $B B_{1} P ▵$ egyenlőszárú derékszögű háromszögek és egybevágók. Ugyanis az $A$ csúcsból kiinduló és $B$ csúcsból kiinduló négyzetek oldalai $O$ -tól egyenlő távolságra vannak: $O A_{1} = O B_{1}$ , és így $A A_{1} = B B_{1}$ ; másrészt az $A A_{1} P ▵$ és $B B_{1} P ▵$ derékszögű háromszögek hegyes szögei $45^{\circ}$ -úak (mert $O A P ∢ = O B P ∢ = 45^{\circ}$ ). Ezért tehát $A_{1} P = B_{1} P$ és így a sokszög oldalai egyenlők; ¹ a sokszög szögei pedig $135^{\circ}$ -úak.

Takács Lajos (kir. kath. rg. VI. o. Dombóvár)

2^{\circ}

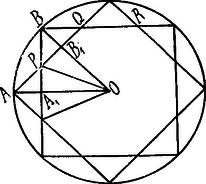. A szóban forgó szabályos nyolcszög területét megkapjuk, ha az

O A_{1} P ▵

területét 16-szorosan vesszük. Az

O A_{1} P ▵

területe

\begin{matrix} t = \frac{1}{2} O A_{1} \cdot A_{1} P = \frac{1}{2} O A_{1} \cdot A A_{1} = \frac{1}{2} O A_{1} (O A - O A_{1}) . \end{matrix}

Azonban

O A = r

és

O A_{1} = \frac{r \sqrt[]{2}}{2}

(t. i. a négyzet oldalának fele).
Eszerint

\begin{matrix} t = \frac{1}{2} \cdot \frac{r \sqrt[]{2}}{2} (r - \frac{r \sqrt[]{2}}{2}) = \frac{r^{2} (\sqrt[]{2} - 1)}{4} \end{matrix}

és így

\begin{matrix} t_{s} = 16 \frac{r^{2} (\sqrt[]{2} - 1)}{4} = 4 r^{2} (\sqrt[]{2} - 1) . \end{matrix}

Bányász István (kegyesrendi fg. V. o. Bp.)

P B_{1} = B O_{1}

stb.