Kezdőlap


Feladat:	90. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csalán E. , Gregor A. , Hajós Gy. , Klein Eszter , Lemberger Klára , Mok Márta , Schlégl Gy. , Sveiczer Márton , Vass B. , Wachsberger Márta , Weisz Lili
Füzet:	1926/február, 165 - 166. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1925/december: 90. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A $P$ pontból a körhöz húzott egyik érintő érintési pontja legyen 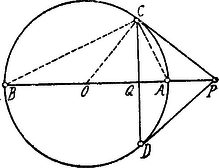$C$ .

P C Q

derékszögű háromszögben, ismert tétel szerint

\begin{matrix} P O : C O = C O : Q O \end{matrix}

és ebből

\begin{matrix} (P O + C O) : (P O - C O) = (C O + Q O) : (C O - Q O) . \end{matrix}

Azonban:

\begin{matrix} P O + C O = P O + O B = P B; P O - C O = P O - A O = P A . \\ C O + Q O = B O + Q O = B Q; C O - Q O = A O - Q O = A Q \end{matrix}

tehát:

\begin{matrix} P B : P A = B Q : A Q, \end{matrix}

vagy tekintettel az irányra is:

\begin{matrix} B P : A P = B Q : A Q . \end{matrix}

Sveiczer Márton (egri áll. főreál VI. o.)

II. Megoldás. A

P C Q ∢

-et oly kerületi szögnek tekinthetjük, melynek egyik szára a

C D

húr, a másik a

P C

érintő és így a

\hat{C A D}

ívhez tartozik; ezt az ívet

C A

felezi, tehát

C A

P C Q ▵

egyik belső szögfelezője. Minthogy

C B ⊥ C A

azért

C B

P C Q ▵

külső szögfelezője; a

C

csúcsból kiinduló szögfelezők talppontjai

A

és

B

, a háromszög alapjának végpontjai:

P

és

Q

, harmonikus pontpárok.

Weisz Lili (izr. leánygimn. VI. o. Bp.)