Feladat: 73. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bányász I. ,  Biermann L. ,  Grünhut P. ,  Hajós Gy. ,  Izr. gimn. V. o. Debrecen. ,  Szombathy M. 
Füzet: 1925/december, 107 - 108. oldal  PDF  |  MathML 
Témakör(ök): Párhuzamos szelők tétele, Diszkusszió, Gyakorlat
Hivatkozás(ok):Feladatok: 1925/október: 73. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A és B pontok az egyenest 3 részre osztják és így M pont 3 féle helyzetet foglalhat el: A és B között, AB-n kívül: vagy az A felőli vagy a B felőli részen.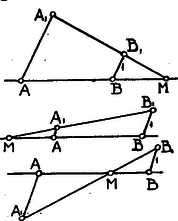

 
 

Minthogy MA:MB=k:1, A és B pontokból rajzoljunk két párhuzamos egyenest; ha k>0, ugyanazon irányban, ha k<0, ellenkező irányban. Az A-ból vont egyenesre mérjünk k, a B-ből vont egyenesre 1 hosszegységet; ezek végpontjai legyenek A1 ill. B1. Már most A1B1 egyenes az AB egyenest a keresett M pontban metszi.
1.Hak=0,akkorMpontA  pontban esik.2.,,0<k<1,,,,,az egyenesnekA  felőli oldalára esik.3.,,k=1,,,,,,,végtelenben fekvő pontja lesz.4.,,k>1,,,,,,,B  felőli oldalára esik.5.,,k=±∞,,,,,a  B  pontba esik.6.,,k<0,,,,,A  és  B  közé esik;;,,k=-1,,,,,az  AB  távolság felezőpontja lesz.
 

Izr. gimn. V. o. Debrecen.

 

Jegyzet. A feladat tárgyalásából kitűnik, hogy az MA és MB távolságoknál az irány is szerepet játszik: MA és MB ellenkező irányúak, ha M pont A és B között van, tehát viszonyuk negatív szám. Oly M pont, melyre nézve az |MAMB| ugyanakkora, kettő van az egyenesen. Ha már most e távolságokat A-tól és B-től számítjuk és
AM1BM1=-AM2BM2,
akkor az (A,B) és (M1,M2) pontpárokat harmonikus pontpároknak nevezzük. A és B az alappontok. M1 és M2 viszonyított pontok. Ilyen harmonikus pontpárok pl. az ABC▵ AB oldalán az A, B csúcsok és a C csúcsból kiinduló belső és külső szögfelezők talppontjai.