Feladat: 50. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Csalán E. ,  Hajós György ,  Kornhauser József ,  Stern J. ,  Sveiczer Márton 
Füzet: 1925/október, 46. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1925/május: 50. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen a három párhuzamos egyenes e1, e2, e3. Vegyük fel pl. e2 egyenesen tetszőlegesen a B ponto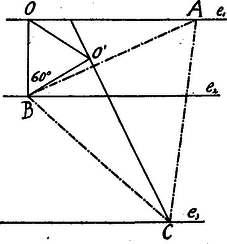t.

 
 

Ha már most B pontot pl. e1 egyenes összes pontjaival összekötve képzeljük és az összekötő távolságok felett egyenlőoldalú háromszögeket szerkesztünk, ezek csúcsainak mértani helye egy egyenes vonal lesz, melyet kapunk, ha e1-t B körül 60∘-kal elforgatjuk. (L. I. évf. 3. sz. 58. oldal 9. feladat.) Ahol ezen mértani hely e3-t metszi, ott lesz C pont. Ezek után e1 egyenesen A pont is meghatározható: BA=BC.
 

Sveiczer Márton (egri áll. főreál V. o.)
 

II. Megoldás. e2 egyenesen felvett B pontból húzzunk egyeneseket, melyek e1, ill. e3-mal 60∘ ill. 120∘-ú szöget alkotnak. Legyenek e szögek csúcsai M (e1-n) 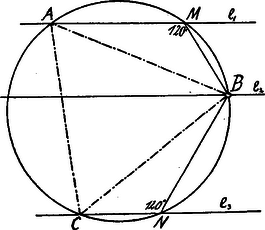és N (e3-n).
 
 

Ha már most az M, B, N pontokon át kört szerkesztünk, ezen kör e1-t A-ban, e3-t C-ben metszi még, ABC∢ egyenlőoldalú lesz. Ugyanis AMBC húrnégyszögben
ACB∢=180∘-120∘=60∘
ABNC húrnégyszögben
BAC∢=180∘-120∘=60∘.

Ezért ABC∢ szintén 60∘.
 

Kornhauser József (egri áll. főreál VI. o.)
 

III. Megoldás. Ha M és N pontokat az előbbi szerint megkaptuk, legyen MA=BN és NC=BM. Felmérve tehát MA-t és NC-t, BMAΔ≅BNCΔ (két oldal és a közbezárt szög egyenlő) és így BA=BC, továbbá MAB∢=NBC∢ és MBA∢=NCB∢. Másrészt MAB∢+MBA∢=60∘ és így NBC∢+MBA∢=60∘. Az e2 egyenes MBN szöget ‐ a párhuzamos egyenesek által létesített váltószögek egyenlősége folytán ‐ két 60∘-ú részre osztja, tehát MBN∢=120∘.
ABC∢=MBN∢-(NBC∢+MBA∢)=120∘-60∘=60∘. Mivel BA=BC és 60∘-ú szög van közöttük, ABC▵ egyenlőoldalú.
 

Hajós György (kegyesrendi fg. IV. B. o. Bp.)