Kezdőlap


Feladat:	37. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Elek T. , Lemberger K. , Tóvárosi Fischer György , Wachsberger M.
Füzet:	1925/szeptember, 13 - 14. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1925/április: 37. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Ha az adott átfogó $c$ , a nagyobbik befogó $x$ , a kisebbik $y$ , akkor e követelmény értelmében

\begin{matrix} x^{2} = c y \end{matrix}

(1)

Ha az

x

vetülete az átfogón

z

y

-é

c - z

, akkor Euklides tételével

\begin{matrix} x^{2} = c z \end{matrix}

(2)

(1) és (2)-ből következik, hogy

\begin{matrix} z = y \end{matrix}

(3)

Ugyancsak Euklides tételével

\begin{matrix} y^{2} = c (c - z) \end{matrix}

(4)

és így tekintettel (3)-ra

\begin{matrix} z^{2} = c (c - z) \end{matrix}

(5)

azaz az átfogót a derékszög csúcsából bocsátott merőleges oly két részre osztja, melyek közül nagyobbik mértani középarányosa az átfogónak és a kisebbik résznek. Tehát az átfogót az ,,aranymetszés'' szabálya szerint kell két részre osztani. De ezen felosztás tulajdonképen az (5) egyenlet megoldásának a szerkesztése. Ezen egyenlet két gyöke közül a negatív nem jöhet itt tekintetbe. A pozitív gyök

\begin{matrix} z = + \sqrt[]{c^{2} + \frac{c^{2}}{4}} - \frac{c}{2} = c \frac{\sqrt[]{5} - 1}{2} \end{matrix}

(6)

\sqrt[]{c^{2} + \frac{c^{2}}{4}}

jelenti azon derékszögű háromszög átfogóját, melynek befogói

c

és

\frac{c}{2}

; ebből az átfogóból ki kell vonni

\frac{c}{2}

-t.

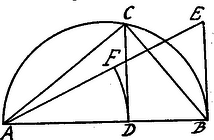
Ha tehát az ábra szerint

A B = c

és

B E ⊥ A B

, továbbá

B E = \frac{c}{2}

, akkor

A E

-ből kivonva

E F = \frac{c}{2}

-t,

A F = z

. Legyen

A D = A F

. A

D

pontban emelt merőleges az

A B

átmérőhöz tartozó félkört a keresett

C

csúcsban metszi. ‐ A (6), (3) és (1) egyenletek alapján kimondhatjuk, hogy:

\begin{matrix} y = z = c \frac{\sqrt[]{5} - 1}{2}; x = c \sqrt[]{\frac{\sqrt[]{5} - 1}{2}} . \end{matrix}

Tóvárosi Fischer György (ev. főgimn. VI. o. Bp.)

Jegyzet. Az ,,aranymetszés'' v. folytatólagos osztásnak nevezetes tulajdonsága, hogy ha ‐ a fenti jelzéseket megtartva ‐

z^{2} = c (c - z)

, akkor egyszersmind

\begin{matrix} {(c - z)}^{2} = z [z - (c - z)] \end{matrix}

azaz a

c

távolság arany metszésénél keletkező kisebbik rész

(c - z)

, a nagyobbik

(z)

részt ismét folytatólagosan osztja. Ugyanis

{(c - z)}^{2} = c^{2} - 2 c z + z^{2}

;

z^{2} = c (c - z)

egyenletből

c^{2} = z^{2} + c z

értéket helyettesítve

\begin{matrix} {(c - z)}^{2} = z^{2} + c z - 2 c z + z^{2} = 2 z^{2} - c z = z (2 z - c) = z [z - (c - z)] . \end{matrix}