Kezdőlap


Feladat:	1499. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bizám György , Bolgár I. , Csáki Frigyes , Csuri V. , Egger Géza , Freud Géza , Hoffmann Tibor , Josepovits Gyula , Káli L. , Klein József , Lax Péter , Máté I. , Sándor Gyula , Volena-Koczor Imre
Füzet:	1939/május, 220 - 221. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Feuerbach-kör, Magasságpont, Körülírt kör középpontja, Diszkusszió, Síkgeometriai szerkesztések, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1939/február: 1499. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a $H$ magassági pontnak az oldalakra vonatkozó tükörképei a körülírt körön feküsznek. Legyen $H$ tükörképe $B C$ oldalra vonatkozólag $H_{1}$ . Kössük össze $O$ -t $H_{1}$ -val; $O H_{1}$ a $B C$ oldalt $P_{1}$ -ben metszi. $P_{1}$ az ellipszis pontja, mert ‐ a szimmetria miatt ‐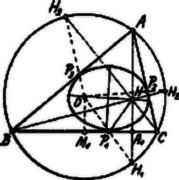

\begin{matrix} P_{1} H_{1} = P_{1} H, tehát O P_{1} + P_{1} H = O P_{1} + P_{1} H_{1} = R, \end{matrix}

azaz a

P_{1}

pontnak az

O

és

H

gyújtópontokból való távolságainak összege az ellipszis nagytengelyével

(R)

egyenlő. Azonban

B C

felezi a

H P_{1} H_{1} ∢

-et és így

B C

az ellipszist a

P_{1}

pontban érinti.

Ha tehát az

O

pontot összekötjük a

H

pontnak az

A B C △

oldalaira való tükörképeivel, az összekötő egyenesek a háromszög oldalait a szóbanforgó ellipszis érintési pontjaiban metszik.
Az

O H

távolság

F

felezőpontja az

A B C △

Feuerbach-körének középpontja, a szóbanforgó ellipszis középpontja. A Feuerbach-kör átmérője az

A B C △

köré írt kör sugarával egyenlő; eszerint az

A B C △

Feuerbach-köre az ellipszis főköre.
A Feuerbach-kör keresztülmegy a

B C

oldal

M_{1}

felezőpontján és az

A H

magasság

A_{1}

talppontján. Mint az ellipszis főköre, keresztülmegy a gyújtópontoknak (

O

és

H

) az érintőn való vetületein (

M_{1}

és

A_{1}

Egger Géza (Fáy András g. VII. o. Bp. IX.)

Jegyzet. I. Az ellipszis tulajdonságai közé tartozik, hogy a gyújtópontoknak valamely érintőtől való távolságainak szorzata állandó, a fél kis tengely négyzetével egyenlő.
Az adott esetben a félnagytengely

\frac{R}{2}

, a lineáris excentricitás fele

\frac{O H}{2}

.
Ki kell mutatnunk tehát, hogy

\begin{matrix} \bar{O M_{1}} \cdot {\bar{H A}}_{1} = \frac{R^{2} \cdot {\bar{O H}}^{2}}{4} . \end{matrix}

Ismeretes, hogy

O M_{1} = \frac{A H}{2}

; továbbá

H A_{1} = \frac{H H_{1}}{2}

.
Eszerint

O M_{1} \cdot H A_{1} = \frac{A H \cdot H H_{1}}{4}

.
Azonban

\bar{A H} \cdot \bar{H H_{1}}

H

pont hatványának abszolut értéke a háromszög köré írt körre nézve és így

\begin{matrix} \bar{A H} \cdot \bar{H H_{1}} = R^{2} - {\bar{O H}}^{2}, azaz {\bar{O M}}_{1} \cdot {\bar{H A}}_{1} = \frac{R^{2} - {\bar{O M}}^{2}}{4} . (Q . e . d .) \end{matrix}

II. Az

A B C △

köré írt kör a szóbanforgó ellipszis egyik vezérköre. V. ö. az 1478. feladat II. megoldását, évfolyamunk 6. számában.
III. Fel kellett tételeznünk, hogy a háromszög hegyesszögű; ha egyenlő oldalú, akkor az ellipszisből kör lesz. (

O

és

H

összeesik.)
Ha a háromszög derékszögű, pl. a

C

csúcsnál, akkor

H \equiv C

és

O H = O C = R

. Az ellipszis gyújtópontjai a nagy tengely végpontjaiba esnek, tehát az ellipszis egy egyenes vonaldarabbá zsugorodik össze

(O C)

.
Ha a háromszög tompaszögű, akkor

H

a körülírt körön kívül fekszik, azaz

O H > R

. Ekkor a háromszög oldalai nem ellipszist érintenek, hanem hiperbolát, amelynek

P

pontjaira nézve

| O P - H P | = R

.
IV. Ha a háromszögbe írt ellipszis egyik gyújtópontja a háromszög

H

magassági pontja, akkor ebből már következik, hogy a másik gyújtópont a körülírt kör

O

középpontja és így az ellipszis nagy tengelye

R

, a körülírt kör sugara. Ugyanis a

H

pontnak az oldalakon, mint az ellipszis érintőin való vetületei meghatározzák a háromszög Feuerbach-körét, mint az ellipszis főkörét. Ennek átmérője a körülírt kör

R

sugarával egyenlő.
A háromszög Feuerbach-köre keresztülmegy az oldalak felezőpontjain: ezek tehát az ellipszis másik gyújtópontjának vetületei az érintőkön. Eszerint a másik gyújtópont a háromszög köré írt kör

O

középpontja.