Kezdőlap


Feladat:	1495. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Baán Sándor , Bizám György , Bolgár I. , Csáki Frigyes , Deák A. , Egger G. , Freud Géza , Hoffmann Tibor , Horváth S. , Josepovits Gyula , Káli L. Tibold , Klein J. , Laub Gy. , Lőke Endre , Margulit György , Máté I. , Nádler M. , Relle F. , Sellmann Tibor , Taksony György , Volena-Koczor Imre
Füzet:	1939/május, 214 - 216. oldal		PDF \| MathML
Témakör(ök):	Kúpszeletek érintői, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1939/február: 1495. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Derékszögű koordinátarendszerünk $X$ -tengelye legyen a parabola tengelye, $Y$ -tengelye a parabola csúcsérintője; ezen rendszerben a parabola egyenlete:

\begin{matrix} y^{2} = 2 p x ... \end{matrix}

(1)

A parabola

M (ξ, η)

pontjában húzott érintő irányhatározója:

\frac{p}{η}

. A parabola

O (0, 0)

pontján átmenő és az előbbi érintőre merőleges egyenes egyenlete:

\begin{matrix} y = - \frac{η}{p} x ... \end{matrix}

(2)

M

ponton és az

F (\frac{p}{2}, 0)

ponton átmenő egyenes egyenlete:

\begin{matrix} \frac{y}{x - \frac{p}{2}} = \frac{η}{ξ - \frac{p}{2}} ill. (ξ - \frac{p}{2}) y = η (x - \frac{p}{2}) ... \end{matrix}

(3)

A (2) és (3) egyenletekből álló egyenletrendszert kielégítő

(x, y)

értékpár a

P

pont koordinátáit szolgáltatja, mint

ξ

és

η

függvényeit.

ξ

és

η

között azonban az

\begin{matrix} η^{2} = 2 p ξ ... \end{matrix}

(4)

összefüggés áll fenn. Hogy a

P

pont

x, y

koordinátái között olyan egyenletet kapjunk, mely nem tartalmazza

ξ

-t és

η

-t, a (2), (3) és (4) egyenletekből kiküszöböljük

ξ

-t és

η

-t.
(2)-ből

η = - p \frac{y}{x}

; (3)-ból

ξ = \frac{p (p - x)}{2 x}

η

és

ξ

ezen értékeit (4)-be helyettesítve:

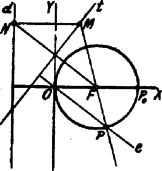\begin{matrix} p^{2} \frac{y^{2}}{x^{2}} = 2 p \frac{p (p - x)}{2 x} ill. x^{2} + y^{2} - p x = 0 ... \end{matrix}

(5)

Eszerint a

P

pont mértani helyének egyenlete:

\begin{matrix} x^{2} + y^{2} - p x = 0. \end{matrix}

Ez oly kört jelent, melynek középpontja a parabola

F (\frac{p}{2}, 0)

gyújtópontja és sugara

\frac{p}{2}

. A kör keresztülmegy az origon.

Baán Sándor (Bencés g. VII. o. Kőszeg.)

Kiegészítés. Ezen körnek az

Y

-tengelyen két pontja van:

O (0,0)

és

P_{0} (p,0)

. Ezek, mint határhelyzetek tartoznak a mértani helyhez. Ha

M

O

-hoz közeledik,

P

P_{0}

-hoz közeledik; ha

M

a végtelen felé tart, akkor

P

O

-hoz közeledik.
[Ugyanis (3)-ból

x - \frac{p}{2} = (ξ - \frac{p}{2}) \frac{y}{η}

.
(2)-ből

\frac{y}{η} = - \frac{x}{p}

, tehát

\frac{2 x - p}{x} = - \frac{1}{p} (2 ξ - p)

.
Ha

ξ = 0, \frac{2 x - p}{x} = 1

és innen

x = p

. Ez a

P_{0}

abscissája.
Ha

ξ \to \infty, \frac{2 x - p}{x} = (2 - \frac{p}{x}) \to \infty

, tehát

x \to 0

. (Ez az

O

).]

II. Megoldás. Legyen a parabola vezérvonala a

d

egyenes, az

M

vetülete

d

-n

N

, tehát

M N = M F

. Ismeretes, hogy a parabola

t

érintője az

M

pontban merőleges

F N

-re. Minthogy

O P ⊥ t

O P ∥ N F

; továbbá

O F ∥ M N

. Ebből következik, hogy

\begin{matrix} O F P ∢ = N M F ∢ és O P F ∢ = N F M ∢, \end{matrix}

tehát

\begin{matrix} O F P △ \sim M N F △ . \end{matrix}

Azonban

N M F △

egyenlőszárú, amelyben

M N = M F

, ezért

O F P △

is egyenlőszárú úgy, hogy

F P = O F = constans

.
Eszerint a

P

pont mértani helye kör, melynek középpontja

F

és sugara

= O F

Káli L. Tibold (Bencés g. VIII. o. Pápa.)

^*Az (5) egyenlet úgy keletkezik, hogy az előbbi mindkét oldalát

x^{2}

-ével szorozzuk.

x^{2} = 0

Y

-tengely egyenlete; azonban az

Y

-tengely nem tartozhatik a mértani helyhez, mert a

P

pontok az

O

ponton átmenő egyenesek pontjai.