Kezdőlap


Feladat:	1486. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ádám L. , Bán Tamás , Bizám György , Boromissza J. , Csáki Frigyes , Csuri Vilmos , Deák András , Engel J. , Fonó András , Freud Géza , Hajnal Miklós , Hoffmann Tibor , Horváth Sándor , Josepovits Gyula , Katona László , Klein József , Laub György , Lengyel S. , Lestál Lajos , Margulit György , Nádler Miklós , Pál Sándor , Rajó Sándor , Sándor Gyula , Taksony György , Volena-Koczor Imre
Füzet:	1939/március, 176 - 178. oldal		PDF \| MathML
Témakör(ök):	Koordináta-geometria, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1939/január: 1486. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Derékszögű koordinátarendszerünk $X$ -tengelye legyen az $A B$ , $Y$ -tengelye az $e$ egyenes. Az $A$ koordinátái $(- d, 0)$ , a $B$ ponté $(d, 0)$ . A változó $R$ pont koordinátái $(0, λ)$ , az $S$ ponté $(0, λ + d)$ .

A R

egyenes egyenlete:

\begin{matrix} y = \frac{λ}{d} (x + d) ... \end{matrix}

(1)

B S

egyenes egyenlete:

\begin{matrix} y = - \frac{λ + d}{d} (x - d) ... \end{matrix}

(2)

A két egyenes metszőpontjának koordinátáit két egyenletből álló egyenletrendszer megoldása szolgáltatja, mint a

λ

paraméter függvényeit. Ha a két egyenletből

λ

-t kiküszöböljük, a metszéspont koordinátái között összefüggést kapunk; ez lesz a keresett mértani hely egyenlete.
1)-ből

λ = \frac{d y}{x + d}

. Ha ezt 2)-be helyettesítjük:

\begin{matrix} y = - \frac{1}{d} (\frac{d y}{x + d} + d) (x - d) ill. (x + d) y = - (y + x + d) (x - d) ... \end{matrix}

(3)

A kijelölt műveletek végrehajtása és összevonása után keletkezik:

\begin{matrix} x^{2} + 2 x y = d^{2} ... \end{matrix}

(4)

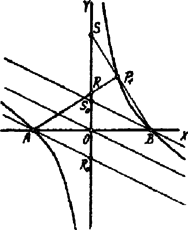
Nyilvánvalóan hiperbolával van dolgunk, melynek középpontja az origó, keresztülmegy az

A

és

B

pontokon,^{$^{*}$} és aszimptotái az

\begin{matrix} x^{2} + 2 x y \equiv x (x + 2 y = 0 ... \end{matrix}

(5)

egyenespárt alkotják. Eszerint a hiperbola egyik aszimptotája az

x = 0

egyenes, azaz az

Y

-tengely, a másik aszimptotája az

x + 2 y = 0

egyenes. (Ennek irányhatározója

- \frac{1}{2}

!)
Ha

R

O

pontban van.

(λ = 0)

, akkor

A R

B S

-t a

B

pontban metszi.

(P \equiv B)

.
Ha

S

van az

O

pontban

(λ = - d)

, akkor

A R

és

B S

metszőpontja,

P \equiv A

.
Ha

R

a végtelenbe jut az

Y

-tengelyen, akkor

A R

és

B S

párhuzamosak az

Y

-tengellyel:

P

Y

-tengely végtelenben fekvő pontja.
Ha

λ = - \frac{d}{2}

, azaz

O

felezi az

R S

távolságot, akkor

A R

és

B S

párhuzamosak és irányhatározójuk:

- \frac{1}{2}

^{$^{*}$}

A R

és

B S

metszőpontja a végtelenben van oly egyenesen, melynek irányhatározója:

- \frac{1}{2}

.
Jelölje az

R, S

pontok helyzetét az utóbbi esetben

R_{0} (0, - \frac{d}{2})

S_{0} (0, \frac{d}{2})

. Ha

R

leírja az

Y

-tengelynek az

R_{0}

feletti részét

(λ > - \frac{d}{2})

, a

P

pont leírja a hiperbola azon ágát, mely az

X

-tengely pozitív oldalán van; ha pedig

R

Y

-tengelyen

R_{0}

-tól

- \infty

felé tart, akkor a

P

pont leírja a hiperbola másik ágát, amely t. i. az

X

-tengely negatív oldalán van.

Freud Géza (Berzsenyi Dániel g. VII. o. Bp. V.)

Jegyzet. a) Ha az (1) és (2) egyenletek rendszerét

x, y

szerint megoldjuk:

\begin{matrix} x = \frac{d^{2}}{2 λ + d}, y = 2 λ \frac{λ + d}{2 λ + d} . \end{matrix}

Ezen paraméteres előállításból kiolvashatók a megállapítások, amelyeket a görbe helyzetére tettünk.
b) Az aszimptoták helyzetét ismerve, megszerkeszthetjük a főtengelyeket.
c) Ha az

R S

távolságnak felső végpontja

R

, akkor a

P

pont az

\begin{matrix} x^{2} - 2 x y = d^{2} \end{matrix}

görbét írja le. Ennek aszimptotái az

x = 0

és

x - 2 y = 0

egyenesek.

^{$^{*}$}

(- d, 0)

és

(d, 0)

kielégítik a (4) egyenletet!

^{$^{*}$}Ha $λ = - \frac{d}{2}$ , akkor az (1) egyenlet átmegy ebbe: $y = - \frac{1}{2} (x + d)$ , míg a (2) ebbe: $y = - \frac{1}{2} (x - d)$ .