Kezdőlap


Feladat:	1472. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bán T. , Bizám György , Csáki Frigyes , Deák András , Engel J. , Hoffmann Tibor , Klein József , Lőke Endre , Margulit György , Máté I. , Pál Sándor , Petricskó M. , Petrovics J. , Pfeifer Béla , Sándor Gyula , Sellmann Tibor , Szittyai Dezső , Taksony György
Füzet:	1939/február, 144 - 146. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Trigonometria, Komplex számok trigonometrikus alakja, Komplex számok tulajdonságai, Feladat
Hivatkozás(ok):	Feladatok: 1938/december: 1472. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Keressük meg az $A$ és $B$ számoknak megfelelő pontokat a számsíkon és szerkesszük meg az $O A B C$ parallelogrammát. Ekkor a $C$ pontnak megtelelő komplex szám $C = A + B$ . Az $O C$ távolság $M$ felezőpontjának pedig $\frac{1}{2} C = \frac{1}{2} (A + B)$ felel meg, azaz az $A$ és $B$ számok számtani középarányosa.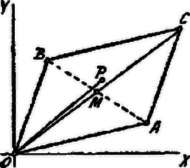

Legyen

A

és

B

mértani középarányosa

P

, tehát, ha

\begin{matrix} A = r_{1} (cos α + i sin α), B = r_{2} (cos β + i sin β), \end{matrix}

akkor

\begin{matrix} P = {(A B)}^{\frac{1}{2}} = {(r_{1} r_{2})}^{\frac{1}{2}} (cos \frac{α + β}{2} + i sin \frac{α + β}{2}), \end{matrix}

azaz

P

argumentuma

\frac{1}{2} (α + β)

és így

O P

felezi az

\hat{A O B}

-et. (Az

A O B

szögről van szó ‐ A szerk.)
Az

\frac{M}{P}

hányados akkor és csak akkor valós, ha az

O

M

P

pontok egy egyenesen vannak. A szóban forgó esetben ez kétféleképpen állhat elő:
1) Az

O

A

B

pontok egy egyenesben vannak, azonban

O

nem fekszik

A

és

B

között¹; ebbe az egyenesbe esnek a

C

M

P

pontok is. Ekkor tehát

\frac{A}{B}

valós.
2) Az

O A B C

parallelogramma

O M C

átlója és

O P

szögfelezője összeesik; tehát, ha

A ‡ B

, kell, hogy

O A B C

rombus legyen,
azaz

\begin{matrix} O A = O B, ill. | A | = | B | . \end{matrix}

II. Megoldás. Ha

A = r_{1} (cos α + i sin α)

B = r_{2} (cos β + i sin β)

, akkor

\begin{matrix} \frac{A + B}{2 {(A B)}^{\frac{1}{2}}} = \frac{r_{1} (cos α + i sin α) + r_{2} (cos β + i sin β)}{2 {(r_{1} r_{2})}^{\frac{1}{2}} [cos \frac{α + β}{2} + i sin \frac{α + β}{2}]} = \\ = \frac{1}{2 {(r_{1} r_{2})}^{\frac{1}{2}}} [r_{1} (cos \frac{α - β}{2} + i sin \frac{α - β}{2}) + r_{2} (cos \frac{β - α}{2} + i sin \frac{β - α}{2})] = \\ = \frac{1}{2 {(r_{1} r_{2})}^{\frac{1}{2}}} [r_{1} cos \frac{α - β}{2} + r_{2} cos \frac{α - β}{2} + i (r_{1} sin \frac{α - β}{2} + r_{2} sin \frac{β - α}{2})] . \end{matrix}

Ezen szám valós, ha

i

szorzója eltűnik, azaz ha:

\begin{matrix} r_{1} sin \frac{α - β}{2} + r_{2} sin \frac{β - α}{2} = (r_{1} - r_{2}) sin \frac{α - β}{2} = 0. \end{matrix}

Ez két esetben következik be:
1 ) Ha

r_{1} - r_{2} = 0

, vagyis

r_{1} = r_{2}

| A | = | B |

.
2) Ha

sin \frac{α - β}{2} = 0

, ill.

\frac{α - β}{2} = k π

α - β = 2 k π (k = 0, \pm 1, \pm 2, ...)

².
Ekkor

\begin{matrix} \frac{A}{B} = \frac{r_{1}}{r_{2}} [cos (α - β) + i sin (α - β)] = \\ = \frac{r_{1}}{r_{2}} [1 + i \cdot 0] = \frac{r_{1}}{r_{2}} azaz \frac{A}{B} valós. \end{matrix}

Sellmann Tibor (Somssich Pál rg. VIII. o. Kaposvár).

Jegyzet.

1^{0}

. A megoldások egy része a komplex számok

a + b i

alakjából indul ki.

2^{0}

. Ha

r_{1} = r_{2} = r

, akkor

\begin{matrix} \frac{A + B}{2} = \frac{1}{2} r [cos α + cos β + i (sin α + sin β)] = r (cos \frac{α + β}{2} cos \frac{α - β}{2} + \\ + i sin \frac{α + β}{2} cos \frac{α - β}{2}) = r cos \frac{α - β}{2} (cos \frac{α + β}{2} + i sin \frac{α + β}{2}) . \end{matrix}

Az I. megoldás szerint

| \frac{A + B}{2} | = O M

. Rombus esetén

O M = r cos \frac{α - β}{2}

és argumentuma

\frac{α + β}{2}

\begin{matrix} | \sqrt[]{A B} | = O P = r \end{matrix}