| Feladat: | 1460. matematika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Freud Géza , Grünfeld Sándor , Jakab Gábor , Josepovits Gy. , Lőke Endre , Sándor Gyula , Volena-Koczor Imre | ||
| Füzet: | 1938/december, 99 - 100. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Terület, felszín, Függvényvizsgálat differenciálszámítással, Feladat, Kúpok, Csonkakúp | ||
| Hivatkozás(ok): | Feladatok: 1938/október: 1460. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az pontban húzott érintőn a csúcs vetülete legyen , a csúcsé , a oldalt felező ponté . 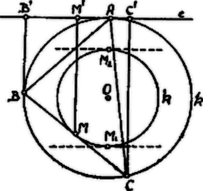 Vizsgálatunknál elsősorban a háromszög oldala állandónak tekintendő. Ha , az sugarú kör állandó hosszúságú húrja, akkor ennek felezőpontja az adott körrel koncentrikus kört ír le. A körnek az érintőre merőleges átmérője a kört oly , pontokban metszi, melyek közül az az -től legtávolabb, a legközelebb van. Ha már most a oldallal szemben hegyes szög fekszik, , akkor és így legnagyobb értéke akkor áll elő, ha az -ben van és . Ekkor az egyenlőszárú és Ha a oldallal szemben tompaszög fekszik, ez ; akkor -nek és így -nek is minimuma áll elő, ha és így . Az egyenlőszárú és most Ha pedig , ekkor ; az oldal felezőpontja mindenkor a kör középpontja és , Amint látjuk, a forgási felület maximumáról állandó esetén akkor lehet szó, ha olyan egyenlőszárú háromszög, amelynek az alappal szemben hegyes szöge van. Jelölje ezen háromszög területét, akkor A körbeírt egyenlőszárú háromszögek között azonban az egyenlőoldalú háromszögé a legnagyobb; ennek értéke . Eszerint Ezen forgási felszínt akkor kapjuk, ha a körbe írt egyenlő oldalú háromszög egyik csúcsa. Jegyzet: Ha az hosszúságú húr kerületi szöghöz tartozik, akkor és Legyen és vizsgáljuk az 1) ha azaz . Ekkor , ; 2) ha , , . Ezt az esetet kizártuk! A 2) eset azt jelentené, hogy az az pontba zsugorodik össze és . Az 1) esetben az helyen pozitív értékekből megy át negatív értékekbe; itt -nak maximuma van. Ezen esetben az egyenlőoldalú és |