Kezdőlap


Feladat:	1458. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bizám György , Csáki Frigyes , Csuri Vilmos , Fonó András , Freud Géza , Hoffmann Tibor , Horváth M. , Josepovits Gy. , Láng S. , Lőke Endre , Nádler Miklós , Sándor Gyula , Szittyai Dezső , Taksony György
Füzet:	1938/december, 97 - 98. oldal		PDF \| MathML
Témakör(ök):	Körök, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1938/október: 1458. matematika feladat

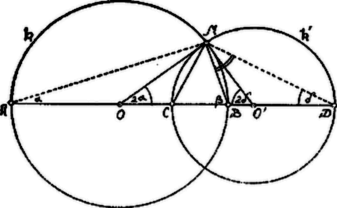
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Szerkesszük meg azon $P$ pontok mértani helyét, amelyekre nézve $\frac{A P}{B P} = m$ , állandó. Ezen mértani hely kör, mely az $A B$ egyenest két pontban metszi: $C$ és $D$ -ben. Ha $C$ $A$ és $B$ között van, akkor $D$ az $A B$ szeleten kívül és $B$ -hez közelebb van, ha $m > 1$ .
Az $A B$ átmérő fölött szerkesztett kört jelölje $k$ , a $C D$ átmérőhöz tartozó kör $k'$ . (Ezen $k'$ a szóbanforgó mértani hely.) $k$ középpontja legyen $O$ , $k'$ -é $O'$ . A két kör egyik metszéspontja legyen $M$ . Be kell bizonyítanunk, hogy $O M ⊥ O' M$ . Az $M A B ∢ = α$ , $M B A ∢ = β$ és (Thales tételével) $A M B ∢ = 90^{\circ}$ ; így $α + β = 90^{\circ}$ .

k

körben

M O B ∢

középponti szög az

α

kerületi szög kétszerese:

M O B ∢ = 2 α

.
A

k'

körben

M O' B ∢ = 2 δ

.
Minthogy

β

M D B Δ

külső szöge,

M D

pedig az

A M B Δ

M

csúcsánál fekvő külső szöget felezi ^{$^{*}$} és ezen külső szög

90^{\circ}

-ú,

δ = β - 45^{\circ}

Eszerint

\begin{matrix} M O O' ∢ + M O' O ∢ = M O B ∢ + M O' B ∢ = 2 α + 2 δ = \\ = 2 α + 2 β - 90^{\circ} = 2 (α + β) - 90^{\circ} = 90^{\circ} . \end{matrix}

Ebből következik, hogy

O M O' ∢ = 90^{\circ}

, azaz

O M ⊥ O' M

Jegyzet: E megoldások túlnyomó részben azt mutatták ki, hogy

{\bar{O O'}}^{2} = {\bar{O M}}^{2} + {\bar{O' M}}^{2}

II. Megoldás. Az

\frac{A C}{B C} = \frac{A D}{B D}

egyenlőség írható így is:

\begin{matrix} \frac{A O + O C}{A O - O C} = \frac{A O + O D}{O D - A O} . \end{matrix}

Ebből keletkezik:

\begin{matrix} {\bar{A O}}^{2} = A C \cdot A D . \end{matrix}

Minthogy

\begin{matrix} A O = O M, {\bar{O M}}^{2} = \bar{A C} \cdot A D . \end{matrix}

Ez azt jelenti, hogy

O M

C D

átmérőjű

k'

kört érinti az

M

pontban. Hasonlóan mutatható ki, hogy

O' M

k

kört érinti az

M

pontban. Tehát

O M ⊥ O M'

Taksony György (Ág. ev. g. VIII. o. Bp.)

^{$^{*}$}

M C

belső szögfelező, mert

A C : B C = A M : B M

; felezi az

A M B ∢ = 90^{\circ}

=ot és

M D ⊥ M C