Kezdőlap


Feladat:	1455. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baán Sándor , Ballay L. , Bizám György , Boromissza J. , Csáki Frigyes , Forgács Péter , Freud Géza , Grünbaum I. , Grünfeld Sándor , Hoffmann M. , Hoffmann Tibor , Klein J. , Korzinek J. , Lang I. , Lestál Lajos , Luncz Gy. , Nádler Miklós , Sándor Gyula , Sellmann Tibor , Taksony György
Füzet:	1938/december, 94 - 95. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Feladat, Függvénytranszformációk
Hivatkozás(ok):	Feladatok: 1938/október: 1455. matematika feladat

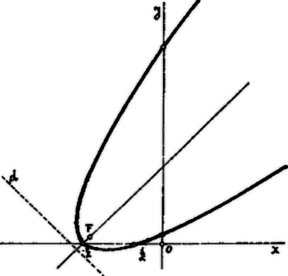
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Állapítsuk meg első sorban a másodfokú görbe nemét. Erre nézve a quadratikus tagok nyújtanak felvilágosítást. Ugyanis ezek

\begin{matrix} 4 (x^{2} - 2 x y + y^{2}) = 4 {(x - y)}^{2} \end{matrix}

(I.)

szerint teljes négyzetet alkotnak, tehát parabolával ‐ esetleg elfajuló parabolával ^{$^{*}$} ‐ van dolgunk, melynek a végtelenben két összeeső pontja van az

x - y = 0

egyenes által meghatározott irányban. Ezen irány azonban a parabola tengelyének iránya. Az

x - y = 0

egyenes irányhatározója

tg α = 1

.
Ha meghatározzuk a parabolának az

X

-, ill.

Y

-tengellyel való metszéspontjait, nyilvánvalóvá válik, hogy a parabola tengelye

α = 45^{\circ}

-ú szöget zár be az

X

tengellyel. ^{$^{*}$}
Állapítsuk meg most a görbe egyenletét oly derékszögű (

x', y'

) koordinátarendszerben, mely az eredetiből, a kezdőpont körüli elforgatásból származik. Az elforgatás szöge pedig legyen

α = + 45^{\circ}

. Ha valamely pont koordinátái az eredeti rendszerben (

x, y

), az új rendszerben (

x', y'

), akkor az ú. n. transzformációs összefüggések:

\begin{matrix} x = x' cos α - y' sin α = x' cos 45^{\circ} - y' sin 45^{\circ} = \frac{\sqrt[]{2}}{2} (x' - y') \\ y = x' sin α + y' cos α = x' cos 45^{\circ} + y' sin 45^{\circ} = \frac{\sqrt[]{2}}{2} (x' + y') . \end{matrix}

Helyettesítsünk ezek szerint a görbe egyenletébe; keletkezik:

\begin{matrix} 2 {(x' - y')}^{2} - 4 (x'^{2} - y'^{2}) + 2 {(x' + y')}^{2} + 4 \sqrt[]{2} (x' - y') - 8 \sqrt[]{2} (x' + y') + 3 = 0. \end{matrix}

Összevonás után:

\begin{matrix} 8 y'^{2} - 4 \sqrt[]{2} x' - 12 \sqrt[]{2} y' + 3 = 0 \end{matrix}

vagy

\begin{matrix} x' = \sqrt[]{2} y'^{2} - 3 y' + \frac{3}{4 \sqrt[]{2}} \\ \frac{x'}{\sqrt[]{2}} = y'^{2} - \frac{3}{\sqrt[]{2}} y' + \frac{3}{8} = {(y' - \frac{3}{2 \sqrt[]{2}})}^{2} - \frac{3}{4} ... & (II.) \end{matrix}

Ebből az egyenletből már világosan látjuk, hogy oly parabolával van dolgunk, melynek tengelye párhuzamos az új koordinátarendszer

X'

-tengelyével; csúcspontjának koordinátái

\begin{matrix} y'_{0} = \frac{3}{2 \sqrt[]{2}}, x'_{0} = - \frac{3}{2 \sqrt[]{2}} . \end{matrix}

A csúcspont koordinátái az eredeti rendszerben

\begin{matrix} x_{0} = \frac{\sqrt[]{2}}{2} (x'_{0} - y'_{0}) = \frac{\sqrt[]{2}}{2} (- \frac{3}{2 \sqrt[]{2}} - \frac{3}{2 \sqrt[]{2}}) = - \frac{3}{2}, \\ y_{0} = \frac{\sqrt[]{2}}{2} (x'_{0} + y'_{0}) = \frac{\sqrt[]{2}}{2} (- \frac{3}{2 \sqrt[]{2}} + \frac{3}{2 \sqrt[]{2}}) = 0, \end{matrix}

azaz a parabola csúcspontja az

X

-tengelyen fekszik.
A parabola tengelyének egyenlete ‐ az (

x

y

) rendszerben:

\begin{matrix} y = x + \frac{3}{2} . \end{matrix}

A parabola megszerkesztéséhez ismernünk kell még a gyújtópont helyzetét. A II. egyenletből kiolvashatjuk, hogyha a parabola paramétere

p

, akkor

\begin{matrix} 2 p = \frac{1}{\sqrt[]{2}}, p = \frac{1}{2 \sqrt[]{2}}, \frac{p}{2} = \frac{1}{4 \sqrt[]{2}} . \end{matrix}

A gyújtópont az

X'

tengellyel párhuzamos egyenesen fekszik, a csúcstól

\frac{p}{2}

távolságban; ezért a gyújtópont koordinátái az (

x', y'

) rendszerben:

\begin{matrix} x'_{1} = - \frac{3}{2 \sqrt[]{2}} + \frac{1}{4 \sqrt[]{2}} = - \frac{5}{4 \sqrt[]{2}}, y'_{1} = \frac{3}{2 \sqrt[]{2}} . \end{matrix}

Az eredeti (

x

y

) rendszerben

\begin{matrix} x_{1} = \frac{\sqrt[]{2}}{2} (- \frac{5}{4 \sqrt[]{2}} - \frac{3}{2 \sqrt[]{2}}) = - \frac{11}{8}, y_{1} = \frac{\sqrt[]{2}}{2} (- \frac{5}{4 \sqrt[]{2}} + \frac{3}{2 \sqrt[]{2}}) = \frac{1}{8} . \end{matrix}

A csúcspont és a gyújtópont meghatározzák a parabola vezérvonalának helyzetét is.

(x + y = - \frac{7}{4})

Csáki Frigyes (Bolyai g. VIII. o. Bp. V.)

^{$^{*}$}Két párhuzamos egyenesből álló egyenespár.

^{$^{*}$}Az $X$ -tengellyel való metszéspontokra nézve $y = 0$ , tehát ezek abscissái I. szerint a $4 x^{2} + 8 x + 3 = 0$ egyenlet gyökei: $- \frac{3}{2}$ és $- \frac{1}{2}$ .
Az $Y$ -tengellyel való metszéspontokra $x = 0$ ; ezek ordinátái I. szerint a $4 y^{2} - 16 y + 3 = 0$ egyenlet gyökei: $2 - \frac{\sqrt[]{13}}{2}$ és $2 + \frac{\sqrt[]{13}}{2}$ .