Kezdőlap


Feladat:	1453. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bán T. , Bizám György , Csáki Frigyes , Deák András , Freud Géza , Grünbaum S. , Grünfeld Sándor , Hajnal Miklós , Halász Iván , Hoffmann Tibor , Horváth M. , Horváth Sándor , Jakab Károly , Josepovits Gyula , Klein J. , Korzinek J. , Lang I. , Lőke Endre , Luncz Gy. , Margulit György , Nádler Miklós , Sándor Gyula , Sellmann Tibor , Steiner Iván , Szabó Béla , Székely Mária , Taksony György , Vásárhelyi Nagy Sándor
Füzet:	1938/december, 91 - 92. oldal		PDF \| MathML
Témakör(ök):	Koordináta-geometria, Síkgeometriai számítások trigonometria nélkül körökben, Feladat, Másodfokú (és arra visszavezethető) egyenletrendszerek, Diszkusszió
Hivatkozás(ok):	Feladatok: 1938/október: 1453. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $M$ pont távolsága az $A B$ -től legyen $M P = y$ , az $A T$ -től $M Q = A P = x$ . Nyilván $y = \sqrt[]{x (2 R - x)}$ , ha $A B = 2 R$ .
Meg kell oldanunk az

\begin{matrix} x + y = l ... & (1) \\ y^{2} = x (2 R - x) ... & (2) \end{matrix}

egyenletekből álló rendszert. (1)-ből

y = l - x

; helyettesítsük ezt (2)-be. Kellő rendezés után keletkezik

\begin{matrix} f (x) \equiv 2 x^{2} - 2 (l + R) x + l^{2} = 0 ... \end{matrix}

(3)

Ezen egyenlet gyöke megfelel a feladatnak, ha valós, pozitív és

l

-nél kisebb,

2 R

-nél nem nagyobb.

(l > 0!)

A (3) gyökei valósak, ha

\begin{matrix} {(l + R)}^{2} - 2 l^{2} \geq 0, (l + R) > l \sqrt[]{2} vagy R \geq l (\sqrt[]{2} - 1) . \end{matrix}

Utóbbi egyenlőtlenség mindkét tagját szorozzuk

(\sqrt[]{2} + 1)

-vel, keletkezik

\begin{matrix} l \leq R (\sqrt[]{2} + 1) ... \end{matrix}

(4)

Vizsgáljuk most a (4) feltételt kielégítve, a (3) gyökeinek helyzetét 0,

l

és

2 R

-hez viszonyítva. Megjegyezhetjük, hogy ha a gyökök valósak, mind a kettő pozitív.

\begin{matrix} f (0) = l^{2} > 0, f (2 R) = {(l - 2 R)}^{2} > 0, f (l) = - l (2 R - l) . \end{matrix}

1^{\circ}

. Ha

l < 2 R

, akkor

f (l) < 0

. A (3) egyenletnek egyik gyöke 0 és

l

között van, a másik

l

és

2 R

között. Az előbbi megfelel, utóbbi nem felel meg. Egy megoldás!

2^{\circ}

. Ha

l = 2 R

, akkor

f (2 R) = 0

. Az egyenlet egyik gyöke

2 R

, a másik

R

. Mindkettő megfelel!

3^{\circ}

. Ha

2 R < l \leq R (\sqrt[]{2} + 1)

, akkor

f (0)

és

f (l)

egyenlő előjelűek. Mind a két gyök 0 és

l

között van, mert a gyökök összegének fele:

\frac{l + R}{2} < l

; ugyanis

R < \frac{l}{2}

.
Ezen esetben tehát mind a két gyök megfelel.

l = R (\sqrt[]{2} + 1)

határesetben a két gyök egyenlő.
Általában:

\begin{matrix} x_{1,2} = \frac{l + R \pm \sqrt[]{{(l + R)}^{2} - 2 l^{2}}}{2} . \end{matrix}

Freud Géza (Berzsenyi Dániel g. VII. o. Bp. V.)

II. Megoldás. Az előbbi eredményeket világítsuk meg geometriai szemlélettel.

x + y = l

oly

I J

egyenes egyenlete, mely az

A B \equiv X

tengelyről és az

A T \equiv Y

tengelyről

l

hosszúságú darabokat vág le e tengelyek pozitív oldalán. Ezen oldalon fekszik az adott kör is, melynek egyenlete: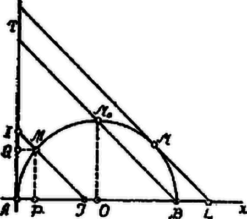

x^{2} + y^{2} = 2 R x

Ha ábránk szerint

A I = A J = l

, az

I J

egyenes keresztülmegy a kör

M

pontján, mely az

X -

tengely felett fekszik.

(A I J ∢ = A J I ∢ = 45^{\circ})

.
Toljuk el az

I J

egyenest önmagával párhuzamosan, amíg a kört az

M'

pontban érinti: ezen érintő lesz az

I J

egyenesek határhelyzete. Ezen határhelyzetben az

X

tengelyt az

L

pontban metszi és

A L = A O + O L = R + R \sqrt[]{2} = R (\sqrt[]{2} + 1)

.
Ha

l < 2 R

, azaz

J

A

és

B

között fekszik, az

I J

egyenes a kört egy pontban metszi az

X

-tengely felett.

l = 2 R

esetben már két

M

pontról lehet szó: az egyik a

B

, a másik az

M_{0}

, mely az

A B

félkört felezi.
Ha

l > 2 R

, de

J

B

és

L

között, akkor az

I J

két pontban metszi a kört, az

X

-tengely felett.

l = A L = R (\sqrt[]{2} + 1)

esetben az

I J

egyenes az

M'

pontban érinti a kört.

(M' abscissája : R + \frac{l - R}{2} = \frac{l + R}{2})

.
Ha

l > A L

, akkor a feltételeknek megfelelő

M

pont nem létezik: az egyenes nem metszi a kört.

Lőke Endre (Premontrei g. VII. o. Keszthely)