Kezdőlap


Feladat:	1448. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bizám György , Bolgár Imre , Csáki Frigyes , Faludy J. , Freud Géza , Grünbaum I. , Grünfeld Sándor , Hajnal Miklós , Hoffmann Tibor , Horkay R. , Jakab Károly , Kaiser K. , Klein József , Kovács L. , Lipsitz Imre , Margulit György , Mészáros György , Ozoróczy György , Sándor Gyula , Sullner László , Szabó Béla , Taksony György , Trunkó I. , Vassányi L. , Volena-Koczor Imre
Füzet:	1938/november, 72 - 73. oldal		PDF \| MathML
Témakör(ök):	Feladat, Mértani helyek, Körérintők
Hivatkozás(ok):	Feladatok: 1938/szeptember: 1448. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $P$ pontból húzható egyik érintő érintési pontja legyen $T_{1}$ . A $P T_{1} \equiv t_{1}$ és $e$ egyenes hegyes szögét felezi az $f_{1}$ , tompaszögüket az $f_{2}$ egyen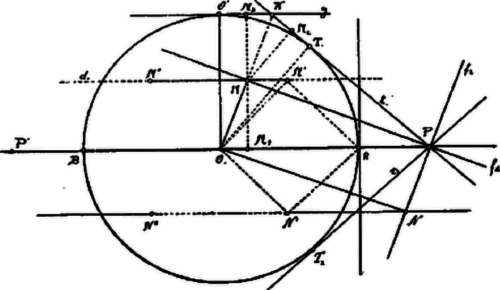es.
$1^{0}$ . A kör $O$ középpontjának vetülete $f_{1}$ -en legyen $M$ . Az $M$ vetülete $e$ -n $M_{1}$ , a $t_{1}$ -en $M_{2}$ . Nyilván $M M_{1} = M M_{2}$ .
A körnek $e$ -vel párhuzamos érintője a $g$ egyenes (az $M$ pont oldalán) a kört az $O'$ pontban érinti: $O O_{1} ⊥ e$ .

O' O T_{1} ∢ = O P T_{1} ∢

, mert száraik merőlegesek egymásra. Hasonló okból

O' O M ∢ = O P M ∢

. Ebből következik, hogy

O M

felezi az

O' O T_{1} ∢

-et és ezért

O M

keresztülmegy a

t_{1}

és

g

érintők

K

metszőpontján és felezi az

O' K P ∢

-et. Az

M

pont tehát egyenlő távolságban a

t_{1}

és

g

egyenesektől, azaz

M M_{2} = M M_{3}

és így

M M_{1} = M M_{3}

.
Minthogy

M M_{3} ⊥ g

és

g ∥ e

, azért

M M_{3} ⊥ e

, tehát

M M_{3}

és

M M_{1}

egy egyenesbe esnek,

M_{1} M_{3} = O O' = r

és így

M M_{1} = \frac{r}{2}

, azaz
az

M

pont távolsága az

e

egyenestől állandó és egyenlő a sugár felével. Az

M

pont az

e

-vel párhuzamos

d_{1}

egyenesen fekszik, melynek távolsága e-től

\frac{r}{2}

.
Vizsgáljuk meg, hogy az

M

pont ezen

e

egyenesnek mely részét írja le?
Ha

P

A

pontban van

(O A = r)

, akkor az érintő merőleges

e

-re. Ezen érintő és az

e

szögét felező egyenesen az

O

vetülete

M'

. Az

O M' A △

hegyes szögei

45^{\circ}

-úak,

M'

távolsága

e

-től

\frac{O A}{2} = \frac{r}{2}

.
Ha

P

A

-ból ez

e

végtelenben fekvő pontja felé tart, az

M

pont a

d_{1}

egyenesen közeledik az

O O'

-hez. Az

f_{1}

és az

e

egyenes szöge folyton kisebbedik: kisebbedik tehát az

O' O M ∢

is. Ha

P

a végtelenbe kerül, akkor az

e

és

f_{1}

szöge, tehát

O' O M ∢

is zérussá válik; az

M

pont ekkor az

O O'

-t felezi.
Ha

P

e

egyenesnek a kör másik oldalán fekvő részét írja le, akkor

M

d_{1}

egyenesnek előbbi darabjával

O O'

-re szimmetrikus részét írja le.
Az

M

pont mértani helye eszerint a

d

egyenesnek

M' M''

darabja, ha

M

O

vetülete az

f_{1}

szögfelezőn.

M' M''

-t az

O O'

telezi;

M'

, ill.

M''

távolsága

O O'

-től

= \frac{r}{2}

2^{0}

f_{2} ⊥ f_{1}

. Az

O

vetülete

f_{2}

-n legyen

N

. Minthogy

O M P N

téglalap,

O P N △ =_{}^{\infty} O P M

. Ebből következik, hogy az

N

pont távolsága

e

-től ugyancsak

\frac{r}{2}

.
Az

N

pont az

e

-vel párhuzamos

d_{2}

egyenesen fekszik, mely

d_{1}

-vel szimmetrikus

e

-re nézve.
Ha

P

A

-ban van, akkor

N'

M'

szimmetrikusa

e

-re nézve. Ha

P

a végtelen felé tart, akkor

N

is a

d_{2}

-n a végtelen felé tart és

P

-vel egyidőben kerül a végtelenbe.
Az

N

pont tehát ‐

O

vetülete az

f_{2}

-n ‐ a

d_{2}

egyenesnek azt a részét írja le, mely

N'

-től a végtelenig terjed, ill. az

O O'

-re szimmetrikus részt,

N''

-től a végtelenig. ‐ Kimarad az

N' N''

darab.
Ha mát most a

P

-ből húzható másik érintőt,

t_{2}

-t vesszük figyelembe, akkor az

O

vetülete a szóbanforgó szögfelezőkön a

d_{1}

és

d_{2}

egyeneseknek azon részeit írja le, amelyek az előbb kimaradtak, amelyek az

M

, ill.

N

pont mértani helyével

e

-re nézve szimmetrikusak. Végeredményben tehát az

O

pontot a négy szögfelezőre vetítve, vetületének mértani helye a

d_{1}

és

d_{2}

párhuzamos egyenesekből álló egyenespár.