Kezdőlap


Feladat:	1444. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Baán Sándor , Bizám György , Bolgár Imre , Boromissza Jenő , Csáki Frigyes , Cseresnyés Zoltán , Csuri Vilmos , Freud Géza , Hajnal Miklós , Hoffmann Tibor , Horváth M. , Juhász Kató , Kaiser K. , Korzsinek J. , Kovács L. , Lang I. , Lestál Lajos , Lipsitz Imre , Luncz Gy. , Margulit György , Mendelsohn György , Puhr L. , Rajó Sándor , Sándor Gyula , Sebők László , Sellmann Tibor , Sulner László , Szlovák István , Taksony György , Vajkóczi J.
Füzet:	1938/november, 67 - 69. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1938/szeptember: 1444. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.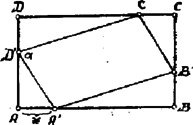

1^{0}

. Legyen

\hat{A' D' C'} = α

. Ábránk szerint

\begin{matrix} α = π - (\hat{A D' A'} + \hat{C' D' D}) . \\ tg α = - tg (\hat{A D' A'} + \hat{C' D' D}) = \\ = - \frac{tg A D' A' + tg C' D' D}{1 - tg A D' A' \cdot tg C' D' D} . \end{matrix}

Azonban

\begin{matrix} tg \hat{A D' A'} = \frac{A A'}{A D'} = \frac{x}{3 a - x}, tg \hat{C' D' D} = \frac{C' D}{D D'} = \frac{5 a - x}{x} . \end{matrix}

Helyettesítve:

\begin{matrix} tg α = - \frac{\frac{x}{3 a - x} + \frac{5 a - x}{x}}{1 - \frac{5 a - x}{3 a - x}} = \frac{2 x^{2} - 8 a x + 15 a^{2}}{2 a x} . \end{matrix}

tg α

kifejezésében a számláló

x

-nek oly másodfokú függvénye, melynek dis-criminánsa negatív. Az ilyen másodfokú függvény állandó előjelű,

x^{2}

együtthatójának előjelével megegyező, tehát az adott esetben

x

minden értékénél pozitív. ^{$^{*}$}. A nevező is pozitív. Eszerint

tg α

pozitív.

α

hegyes szög.
A parallelogramma a téglalapon belül marad; következik ebből, hogy

\begin{matrix} 0 ≦ x ≦ 3 a . \end{matrix}

x = 0

mellett

tg α = \infty

α = \frac{π}{2}

. A parallelogramma összeesik a téglalappal.

x = 3 a

mellett

tg α = \frac{3}{2}

tg α

differenciálhányadosa:

\begin{matrix} \frac{d tg α}{d x} = \frac{(4 x - 8 a) 2 a x - 2 a (2 x^{2} - 8 a x + 15 a^{2})}{4 a^{2} x^{2}} = \frac{2 x^{2} - 15 a^{2}}{2 a x^{2}} . \end{matrix}

Ez negatív, ha

0 ≦ x < a \sqrt[]{\frac{15}{2}}

, pozitív, ha

x > a \sqrt[]{\frac{15}{2}}

és eltűnik, ha

x = a \sqrt[]{\frac{15}{2}}

. Eszerint az

x = a \sqrt[]{\frac{15}{2}} \sim 2, 74 a

helyen

tg α

-nak minimuma van és ezen minimum: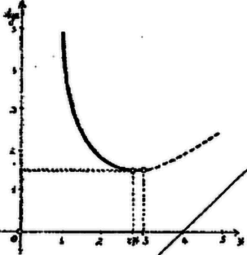

\sqrt[]{30} - 4 \sim 1, 48

A függvény változását jellemző táblázat:

\begin{matrix} x & 0 & 2, 74 a & 3 a \\ (tg α)' & - \infty & - & 0 & + \\ tg α & \infty & ↘ & 1, 48 a & ↗ & \frac{3}{2} \end{matrix}

Írjuk

tg α

értékét a köv. alakban:

\begin{matrix} tg α = \frac{x}{a} - 4 + \frac{15 a}{x} . \end{matrix}

Innen kiolvashatjuk, hogy

tg α

változását ábrázoló görbének egyik aszimptotája az

Y

-tengely, a másik az

y = \frac{x}{a} - 4

egyenes, amelyhez a görbe közeledik, ha

x \to \infty

. A görbének az

x = 0

és

x = 3 a

közötti darabja ábrázolja

tg α

változását. (A görbe egy hiperbola íve!)

2^{0}

. Az

A A' D'

és

C C' B'

háromszögek egybevágók; területük egyenlő és közös értékük

\begin{matrix} \frac{A A' \cdot A D'}{2} = \frac{x (3 a - x)}{2} . \end{matrix}

Hasonlóan a

B B' A'

és

D D' C'

háromszögek mindegyikének területe

\begin{matrix} \frac{B B' \cdot A' B}{2} = \frac{x (5 a - x)}{2} . \end{matrix}

A parallelogramma területét megkapjuk, ha a téglalap területéből kivonjuk a négy derékszögű háromszög területét:

\begin{matrix} y = 3 a \cdot 5 a - x (3 a - x) - x (5 a - x) = 2 x^{2} - 8 a x + 15 a^{2} . \end{matrix}

x = 0

mellett

y = 15 a^{2}

(a téglalap területe).

x = 3 a

mellett

y = 9 a^{2}

.
A területfüggvénynek minimuma van, ha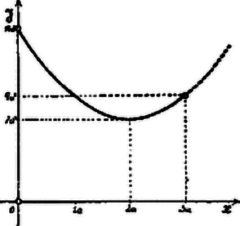

x = 2 a

és

y_{min} = 7 a^{2}

A terület változását egy parabolának íve tünteti fel; ezen ív

x = 0

és

x = 3 a

között fekszik.
Ebből a változásból kitűnik, hogy ha

y = k^{2}

, akkor a

\begin{matrix} 2 x^{2} - 8 a x + 15 a^{2} = k^{2} \end{matrix}

egyenletnek csak akkor van megoldása, ha

7 a^{2} ≦ k^{2} ≦ 15 a^{2}

, ^{$^{*}$}
még pedig két megoldása van, ha

7 a^{2} < k^{2} ≦ 9 a^{2}

egy megoldása van, ha

9 a^{2} < k^{2} ≦ 15 a^{2}

k^{2} = 7 a^{2}

mellett az egyenletnek két összeeső megoldása van.

Hoffmann Tibor (Szent István g. VII. o. Bp. XIV.)

^{$^{*}$}

2 x^{2} - 8 a x + 15 a^{2} = 2 {(x - 2 a)}^{2} + 7 a^{2} > 0

x

minden értékénél!

^{$^{*}$} $k^{2} = 15 a^{2}$ esetben $2 x^{2} - 8 a x = 0$ egyenlet egyik gyöke $x_{1} = 0$ , a másik gyöke $x_{2} = 4 a$ . Utóbbi esetben a parallelogramma nem fekszik a téglalapon belül.