Kezdőlap


Feladat:	1435. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bizám György , Freud Géza , Halász Iván , Hoffmann Tibor , Klein J. , Sándor Gyula , Taksony György
Füzet:	1938/október, 42 - 44. oldal		PDF \| MathML
Témakör(ök):	Kör egyenlete, Koordináta-geometria, Feladat, Pont körre vonatkozó hatványa, Paraméteres egyenletek
Hivatkozás(ok):	Feladatok: 1938/május: 1435. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . Vizsgálatunkból kizárjuk azon esetet, amidőn az $e$ egyenes $(y = 10 - x)$ az $X$ tengelyt $A$ és $B$ között metszi, vagy ezek egyikén megy keresztül. Ha ezen esetekben a $C$ az $X$ tengelyen van, akkor $A C B ∢ = 180^{\circ}$ , és ha $C$ az $e$ egyenesen tovább mozog, ‐ bármelyik irányban ‐, az $A C B ∢$ folyton csökken, és zérussá válik, ha $C$ az $e$ egyenesen a végtelenbe kerül.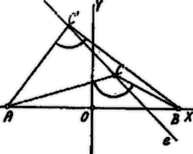

Csakis azon esetet vizsgáljuk, amidőn

A

és

B

e

egyenes ugyanazon oldalán feküsznek; határesetben

e

keresztülmegy az adott pontok egyikén. Az

A

koordinátái legyenek (

- a

, 0), a

B

ponté (

a

, 0), ahol

0 ≦ a ≦ 10

.
Az

y = 10 - x

egyenes az

X

-tengelyt a

K

(10, 0)

, az

Y

-tengelyt az

L (0, 10)

pontban metszi.
Az

A C B ∢ = γ

legnagyobb akkor, ha az

A B C △

köré írt kör az

e

egyenest a

C

pontban érinti.
Keresni kell tehát azon kört, mely az

A

B

pontokon megy keresztül és az

e

egyenest érinti.
Az

A

B

pontokon átmenő kör középpontja az

Y

-tengelyen fekszik; koordinátái:

(0, η)

. Az ilyen kör egyenlete:

\begin{matrix} x^{2} + {(y - η)}^{2} = a^{2} + η^{2} \end{matrix}

vagyis¹

\begin{matrix} x^{2} + y^{2} - 2 η y - a^{2} = 0 ... \end{matrix}

(1)

Ezen kör érinti az

y = 10 - x

egyenest, ha két összeeső közös pontja van. A közös pontok abscissáira nézve

\begin{matrix} x^{2} + {(10 - x)}^{2} - 2 (10 - x) η - a^{2} = 0, \\ ill 2 x^{2} + (2 y - 20) x + 100 - 20 η - a^{2} = 0 ... & (2) \end{matrix}

A körnek és az egyenesnek két összeeső közös pontjuk van, ha a (2) gyökei egyenlők, azaz ha a (2) driscriminánsa eltűnik:

\begin{matrix} D \equiv {(2 y - 20)}^{2} - 8 (100 - 20 η - a^{2}) = 0. \end{matrix}

Rendezve és egyszerűsítve:

\begin{matrix} η^{2} + 20 η + 2 a^{2} - 100 = 0 ... \end{matrix}

(3)

(3)-ból

\begin{matrix} η = - 10 \pm \sqrt[]{2 (100 - a^{2})} . \end{matrix}

(0, η)

oly kör középpontja, mely keresztülmegy az

A

B

pontokon és az

e

egyenest érinti. Ilyen tehát,

a

megadott értéke mellett kettő van. Az érintési pont abscissáját pedig a 2) kétszeres gyöke jelenti; az érintési pontra nézve tehát

\begin{matrix} x = - \frac{2 η - 20}{2} = \frac{10 - η}{2} és y = 10 - x = \frac{10 + η}{2} . \end{matrix}

A (3) gyökei valósak, ha

100 - a^{2} > 0

, azaz

0 ≦ a ≦ 10

, mert

a

nem lehet negatív (L. bevezetésünkben!)
Ha

2 a^{2} - 100 < 0

, vagyis

0 < a < 5 \sqrt[]{2}

, akkor a (3) gyökei ellenkező előjelűek: az egyik kör középpontja az

X

-tengely felett van, a másik az

X

-tengely alatt.
Ha

a = 5 \sqrt[]{2}

, a 3) egyik gyöke zérus, a másik:

- 20

.
Ha

5 \sqrt[]{2} < a < 10

, akkor a (3) mind a két gyöke negatív: mind a két kör középpontja az

X

-tengely alatt van.
Ha

a = 10

, akkor a (3)-nak két egyenlő gyöke van: ekkor a

B

pont összeesik

C

-vel,

η = - 10

és

γ = 180^{\circ}

.
Ha pedig

a = 0

, azaz

A

és

B

O

pontban esnek össze, mindegyik kör érinti az

e

egyenest a

C

, ill.

C'

pontban, az

X

-tengelyt az

O

pontban és ekkor 3)-ból:

η^{2} + 20 η - 100 = 0

, tehát

η = - 10 (1 \pm \sqrt[]{2})

.
Ezen két érték

η

-ra nézve felső és alsó határt jelent: ² az

X

-tengely feletti kör középpontjának távolsága az

X

-tengelytől legfeljebb

- 10 (1 - \sqrt[]{2})

, az

X

-tengely alatti kör középpontjának távolsága az

X

-tengelytől legfeljebb

\begin{matrix} | - 10 (1 + \sqrt[]{2}) | = 10 (1 + \sqrt[]{2}) . \end{matrix}

Jegyzet.

1^{\circ}

. Legyen pl.

r^{2} = 28

.
Ekkor

\begin{matrix} η^{2} + 20 η - 44 = 0 \end{matrix}

és

\begin{matrix} η_{1} = 2, η_{2} = - 22. \end{matrix}

Az érintési pontra nézve, ha

η = 2

, (2) szerint

2 x^{2} - 16 x + 32 = 0

, ill.

{(x - 4)}^{2} = 0

x = 4

;

y = 6

.
Ha pedig

η = - 22

, akkor (2) szerint

\begin{matrix} 2 x^{2} - 64 x + 512 = 0, \end{matrix}

ill.

\begin{matrix} {(x - 16)}^{2} = 0, \end{matrix}

tehát

\begin{matrix} x = 16, y = - 6. \end{matrix}

2^{0}

. Ha az

A

B

pontokon átmenő kör az

e'

egyenest a

C

pontban érinti, akkor ‐

K

pont hatványa e körre vonatkoztatva ‐

\begin{matrix} {\bar{K C}}^{2} = \bar{K A} \cdot \bar{K B} = (10 - a) (10 + a) = 100 - a^{2} . \end{matrix}

Eszerint

K C

értéke változik 0-tól 10-ig. Ezen változással kapcsolatos vizsgálatok az előbbiekkel megegyező eredményre vezetnek.
A

K C

e

egyenesen felrakható két irányban

K

-ból kiindulva, és így jutunk a két körhöz, szerkesztéssel is.

¹A kör keresztülmegy a

(a, 0)

ponton, tehát

a^{2} + η^{2} = r^{2}

²Ugyanis általában $η = - 10 \pm \sqrt[]{2 (100 - a^{2})}$
$η_{1} = - 10 + \sqrt[]{2 (100 - a^{2})}$ legnagyobb értéke akkor áll elő, ha $a = 0$ .
$η_{2} = - 10 - \sqrt[]{2 (100 - a^{2})}$ abszolut értéke legnagyobb, ha $a = 0$ .