Kezdőlap


Feladat:	1430. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Sándor Gyula
Füzet:	1938/szeptember, 18 - 21. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Másodfokú függvények, Egyenes körkúpok, Feladat, Háromszög területe
Hivatkozás(ok):	Feladatok: 1938/április: 1430. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.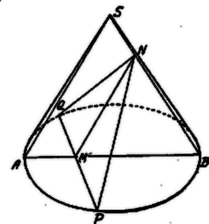

1^{0}

. Minthogy

B M N △ \sim B A S △

M N : A S = B M : B A

M N = \frac{A S \cdot B M}{B A} = \frac{a (2 R - x)}{2 R}

. Az

A P B △ P

-nél derékszögű:

\begin{matrix} \bar{{M P}^{2}} = A M \cdot M B = x (2 R - x) . \end{matrix}

Feltételi egyenletünk:

M N + M P = l

, tehát

\begin{matrix} \frac{a (2 R - x)}{2 R} + \sqrt[]{x (2 R - x)} = l, \end{matrix}

ill.

\begin{matrix} 2 R \sqrt[]{x (2 R - x)} - 2 R (l - a) + a x ... \end{matrix}

(1)

1) baloldala pozitív (határesetben zérus); kell tehát, hogy jobboldala is ilyen legyen, azaz

x ≧ \frac{2 R (a - l)}{a}

. Természetesen

x ≦ 2 R

.
1) mindkét oldalán emeljünk négyzetre és azután rendezzünk; keletkezik:

\begin{matrix} f (x) \equiv (a^{2} + 4 R^{2}) x^{2} - 4 R (2 R^{2} + a^{2} - a l) x + 4 R^{2} (l^{2} - 2 a l + a^{2}) = 0 ... \end{matrix}

(2)

Innen

\begin{matrix} x = \frac{2 R}{a^{2} + 4 R^{2}} (2 R^{2} + a^{2} - a l + 2 R \sqrt[]{R^{2} + a l - l^{2}}) ... \end{matrix}

(3)

A gyökök valósak, ha

l^{2} - a l - R^{2} \leq 0

; ez bekövetkezik, ha

\begin{matrix} \frac{a - \sqrt[]{a^{2} + 4 R^{2}}}{2} < l ≦ \frac{a + \sqrt[]{a^{2} + 4 R^{2}}}{2}, ill. 0 < l ≦ \frac{a + \sqrt[]{a^{2} + 4 R^{2}}}{2} ... \end{matrix}

(4)

minthogy

l

csak pozitív lehet.
Szükséges továbbá, hogy a 2) gyökei pozitívok legyenek,

f (0) = 4 R^{2} {(l - a)}^{2} \geq 0

¹. Ebből következik, hogy

0

a gyökökön kívül fekszik; kisebb a gyököknél, ha a gyökök összege is pozitív, azaz ha

\begin{matrix} 2 R^{2} + a^{2} - a l > 0, ill. l < \frac{2 R^{2} + a^{2}}{a} ... \end{matrix}

(5)

²
Továbbá

f (2 R) = 4 R^{2} l^{2}

, tehát

2 R

is a gyökökön kívül van és ezeknél mindig nagyobb, mert a gyökök félösszege

\begin{matrix} \frac{2 R (2 R^{2} + a^{2} - a l)}{a^{2} + 4 R^{2}} < 2 R, hacsak 2 R^{2} > - a l . \end{matrix}

Ez pedig igaz. Végül

\begin{matrix} f [\frac{2 R (a - l)}{a}] = \frac{16 R^{4} l}{a^{2}} (l - a) . \end{matrix}

Ez negatív, ha

l < a

; ezen esetben

\frac{2 R (a - l)}{a}

f (x) = 0

gyökei között van, tehát csak a nagyobbik gyök felel meg.
Ha azonban

l > a

, mind a két gyök megfelel, mert

\begin{matrix} \frac{2 R (a - l)}{a} < \frac{2 R (2 R^{2} + a^{2} - a l)}{a^{2} + 4 R^{2}} . \end{matrix}

Ugyanis ezen egyenlőtlenséget rendezve,

l > \frac{a}{2}

áll elő; ez pedig igaz, mert

l > a

esetet vettük figyelembe.
Összefoglalva: ha

0 < l < a

, a 2) egyenletnek csak az egyik, t. i. a nagyobbik gyöke felel meg.
Ha

a < l < \frac{a + \sqrt[]{a^{2} + 4 R^{2}}}{2}

, mind a két gyök megfelel.
Ha

l = 0

, akkor a

\frac{2 R (a - l)}{a} ≦ x ≦ 2 R

feltétel az

2 R \leq x \leq 2 R

feltételhez vezet, azaz

x = 2 R

. Tehát, ha

l = 0

, akkor a 2)-nek csak az egyik (a nagyobbik) gyöke felel meg és ez valóban:

x = 2 R

.
Ha

l = a

, akkor

x' = 0

x'' = \frac{8 R^{3}}{a^{2} + 4 R^{2}}

.
Ha

\begin{matrix} l = \frac{a + \sqrt[]{a^{2} + 4 R^{2}}}{2}, x' = x'' = \frac{R (4 R^{2} + a^{2} + \sqrt[]{a^{2} + 4 R^{2}})}{a^{2} + 4 R^{2}} . \end{matrix}

Vizsgáljuk már most

l

változását:

\begin{matrix} l = \frac{a (2 R - x)}{2 R} + \sqrt[]{x (2 R - x)} . \end{matrix}

x = 0

mellett

l = a

. (T. i.

M N = S A = a

M P = 0

x = 2

mellett

l = 0

. (T. i.

M N = 0

és

M P = 0

; az

M

pont

B

-be került.)

\begin{matrix} l' = \frac{d l}{d x} = - \frac{a}{2 R} + \frac{2 (R - x)}{2 \sqrt[]{x (2 R - x)}} = \frac{- a \sqrt[]{x (2 R - x)} + 2 R (R - x)}{2 R \sqrt[]{x (2 R - x)}} . \\ \frac{d l}{d x} = 0, ha a \sqrt[]{x (2 R - x)} = 2 R (R - x) ... & (6) \end{matrix}

A baloldal pozitív; kell, hogy a jobboldal is az legyen. Tehát az egyenletet csak

x < R

érték elégítheti ki.
Négyzetre emelve a 6) mindkét oldalán és rendezve:

\begin{matrix} g (x) \equiv x^{2} - 2 R x + \frac{4 R^{4}}{a^{2} + 4 R^{2}} = 0 ... \end{matrix}

(7)

A gyökök valósak és pozitívok; összegük

2 R

és így az egyik nagyobb, a másik kisebb, mint

R

g (x) = 0

kisebbik gyöke

\begin{matrix} x_{1} = R (1 - \frac{a}{\sqrt[]{a^{2} + 4 R^{2}}}) . \end{matrix}

A szóbanforgó közben, t. i.

x = 0

és

x = 2 R

között,

\frac{d l}{d x}

csak egy esetben tűnik el, t. i. ha

x = x_{1}

. Ezen közben

l

és

\frac{d l}{d x}

x

-nek folytonos függvénye; ha

x < x_{1}

, akkor

\frac{d l}{d x} > 0

, ha

x > x_{1}

, akkor

\frac{d l}{d x} < 0

. Így az

x = x_{1}

helyen

l

-nek maximuma van és ennek értéke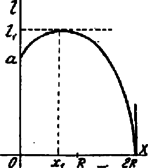

\begin{matrix} l_{1} = \frac{1}{2} (a + \sqrt[]{a^{2} + 4 R^{2}}) . \end{matrix}

l

változását feltünteti a következő táblázat: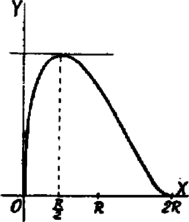

\begin{matrix} \begin{matrix} x & 0 & x_{1} & 2 R \\ l' & \infty & + & 0 & - & - \infty \\ l & a & ↗ & \binom{l_{1}}{{max}_{}^{}} & ↘ & 0 \end{matrix} \end{matrix}

l

változását ábrázoló görbe menetéből igazolhatók az 1), ill. 2) egyenletek diszkussziója közben megállapított eredmények!

2^{0}

. A

P N Q △

területe

\begin{matrix} y = \frac{M N \cdot P Q}{2} = M N \cdot M P = \frac{a}{2 R} (2 R - x) \sqrt[]{x (2 R - x)} . \end{matrix}

y = 0

, ha

x = 0

és ha

x = 2 R

. (

x = 0

mellett a

P N Q △

S A

vonaldarabbá,

x = 2 R

mellett a

B

pontba zsugorodik össze.)

\begin{matrix} y' = \frac{a}{2 R} [- \sqrt[]{x (2 R - x)} + (2 R - x) \frac{2 R - 2 x}{2 \sqrt[]{x (2 R - x)}}] = \\ = \frac{a (2 R - x) (R - 2 x)}{2 R \sqrt[]{x (2 R - x)}} = \frac{a (R - 2 x) \sqrt[]{2 R - x}}{2 R \sqrt[]{x}} . \end{matrix}

y' = 0

, ha

x = \frac{R}{2}

és ha

x = 2 R

; továbbá

y' < 0

ezen két hely között, míg

\begin{matrix} y' > 0, ha 0 < x < \frac{R}{2} . \end{matrix}

Következik ebből, hogy

x = \frac{R}{2}

helyen a függvénynek maximuma van és ennek értéke

y_{{max}_{}^{}} = \frac{2 \sqrt[]{3}}{8} a R

x = 2 R

helyen a görbe érintője az

X

-tengely,

x = 0

helyen az

Y

-tengely.

A függvény változását feltünteti e táblázat:

\begin{matrix} \begin{matrix} x & 0 & R / 2 & 2 R \\ y' & + \infty & + & 0 & - & 0 \\ y & 0 & ↗ & \binom{\frac{3 \sqrt[]{3}}{8} a R}{{max}_{}^{}} & ↘ & 0 \end{matrix} \end{matrix}

Részben megoldotta: Sándor Gy.

¹Egyenlőség áll elő, ha

l = a

. Ekkor a 2) egyik gyöke zérus.

² $\frac{2 R^{2} + a^{2}}{a} > \frac{a + \sqrt[]{a^{2} + 4 R^{2}}}{2}$ . T. i. kellő rendezés után keletkezik:
${({4 R}^{2} + a^{2})}^{2} > a^{2} (a^{2} + 4 R^{2})$ . Ez pedig igaz. Ha tehát $l$ eleget tesz annak a feltételnek, amelynek kielégítése szükséges ahhoz, hogy a gyökök valósak legyenek, akkor az 5) is ki van elégítve.