Kezdőlap


Feladat:	1425. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Egri György , Freud Géza , Sándor Gyula , Weisz Alfréd
Füzet:	1938/szeptember, 14 - 15. oldal		PDF \| MathML
Témakör(ök):	Hiperbola egyenlete, Kúpszeletek érintői, Feladat, Mértani helyek
Hivatkozás(ok):	Feladatok: 1938/április: 1425. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kiindulunk a kúpszeletek azon meghatározásából, amely szerint a kúpszelet mértani helye azon pontoknak, amelyekre nézve egy szilárd ponttól és egy szilárd egyenestől való távolságuk viszonya állandó. Az adott esetben a szilárd pont az origó, a kúpszelet egyik gyújtópontja és a szilárd egyenes a hozzá tartozó vezérvonal; ennek egyenlete $x - d = 0$ .
Valamely $P (x, y)$ pontra nézve az origótól való távolság: ${(x^{2} + y^{2})}^{\frac{1}{2}}$ .
A $P$ pont távolsága az adott egyenestől $| x - d |$ .
$P$ pontnak ki kell elégítenie a következő egyenletet:

\begin{matrix} \frac{{(x^{2} + y^{2})}^{\frac{1}{2}}}{| x - d |} = k ill. x^{2} + y^{2} - λ {(x - d)}^{2} = 0 ... \end{matrix}

(1)

ahol

λ = k^{2}

tetszőleges pozitív szám (ill. zérus), paraméter.^{$^{*}$} Az 1) kúpszelet sereg egyenlete: a seregben vannak ellipszisek, egy parabola és hiperbolák.
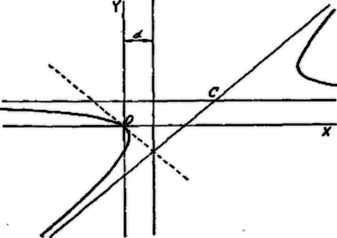
Vizsgáljuk már most ezen kúpszeletek azon pontjait, amelyekhez tartozó érintők párhuzamosak az

y = x

egyenessel, azaz ezen érintők irányhatározója:

1

.
Az 1) egyenletet

x

szerint differenciálva

\begin{matrix} 2 x + 2 y y' - 2 λ (x - d) = 0, ill. x + y y' - λ (x - d) = 0 ... \end{matrix}

(2)

y'

, az érintő irányhatározója

= 1

, akkor az érintési pontok koordinátái között az

\begin{matrix} x + y - λ (x - d) = 0 ... \end{matrix}

(3)

összefüggés áll fenn. Az (1) és (3) egyenletekből álló rendszert

x

és

y

szerint megoldva

x

és

y

, mint

λ

paraméter függvényei állíthatók elő: így az érintési pontok mértani helyének paraméteres egyenleteit kapjuk. Ha pedig az (1)-ből, (3)-ból

λ

-t kiküszöböljük, az érintési pontok

x

y

koordinátái közötti összefüggéshez, a szóbanforgó mértani hely egyenletéhez jutunk.
(3)-ból

λ = \frac{x + y}{x - d}

. Ha ezt (1)-be behelyettesítjük, keletkezik:

\begin{matrix} x^{2} + y^{2} - (x + y) (x - d) = 0 \\ vagy y^{2} - x y + d (x + y) = 0 ... & (4) \end{matrix}

A (4) nyilvánvalóan hiperbola egyenlete; a quadratikus tagok:

y^{2} - x y = y (y - x)

. Ebből azt olvashatjuk ki, hogy e hiperbola aszimptotái az

y = 0

és

y - x = 0

egyenesekkel párhuzamosak. A hiperbola középpontját a

\begin{matrix} - y + d = 0 ... & (5) \\ 2 y - x + d = 0 ... & (6) \end{matrix}

egyenletrendszer határozza meg; a középpont koordinátái:

3 d

d

Eszerint az aszimptoták egyenletei:

\begin{matrix} y = d ... & (7) \\ y = x - 2 d ... & (8) \end{matrix}

(4)-ből következik, hogy az

x + y = 0

egyenes a hiperbolát az origóban érinti. (

y = - x

egyenesnek a 4) hiperbolával két összeeső közös pontja van az origóban!)

^{$^{*}$}

λ = 0

esetben az

x^{2} + y^{2} = 0

(zérus sugarú) körhöz jutunk.