Kezdőlap


Feladat:	1419. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bizám György , Fehér György , Gáspár Rezső , Komlós János , Névtelen , Sándor Gyula , Schreiber Béla
Füzet:	1938/május, 285. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Transzverzálisok, Euler-egyenes, Körülírt kör, A háromszögek nevezetes pontjai, Húrnégyszögek, Körérintési szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1938/március: 1419. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kimutatjuk, hogy az $E_{a} E_{b} E_{c} △$ oldalai párhuzamosak az $M_{a} M_{b} M_{c} △$ oldalaival.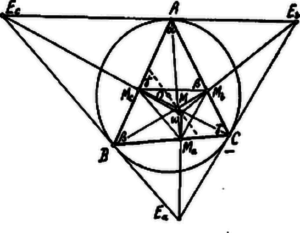

A

pontban, az

A B C △

köré irt körhöz húzott érintő az

A C

oldallal oly kerületi szöget alkot, mely a

β

szög ívéhez tartozik:

E_{b} A C ∢ = β

.
Az

A M_{b} M_{c} △

-ben

A M_{b} M_{c} ∢ = β

. Ugyanis

B C M_{b} M_{c}

húrnégyszög azon körben, melynek átmérője

B C

; ezért

C M_{b} M_{c} ∢ = 180^{\circ} = β

és ennek mellékszöge

A M_{b} M_{c} ∢ = β

. Ezek szerint

E_{b} E_{c} ∥ M_{b} M_{c}

.
Ugyanígy:

E_{c} E_{a} ∥ M_{c} M_{a}

és

E_{a} E_{b} ∥ M_{a} M_{b}

.
Ebből következik, hogy az

E_{a} E_{b} E_{c}

, és

M_{a} M_{b} M_{c}

háromszögek hasonlóak és hasonló helyzetűek: a megfelelő csúcsokat összekötő egyenesek egy ponton, a két háromszög hasonlósági pontján mennek keresztül. Legyen ezen pont

ω

. A két háromszög megfelelő pontjait összekötő egyenesek mindegyike

ω

-n megy keresztül.
Már most az

A B C △

köré írt kör az

E_{a} E_{b} E_{c} △

-re nézve beírt kör; ennek középpontja

O

.
Az

A B C △

magassági pontja

M

, az

M_{a} M_{b} M_{c} △

-re nézve szintén a beírt kör középpontja, hiszen az

A B C △

magassági vonalai az

M_{a} M_{b} M_{c}

talpponti háromszög szögfelezői. Tehát az

O M

egyenes, az

A B C △

Euler-egyenese keresztülmegy

ω

-n:

ω

ezen Euler-egyenesen fekszik.

Gáspár Rezső (Kossuth Lajos g. VIII. o. Pestszenterzsébet.)