Kezdőlap


Feladat:	1409. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Klein József , Komlós János , Méri B. , Sándor Gyula , Sydó Sándor , Szittyai Dezső , Weisz Alfréd
Füzet:	1938/április, 247 - 248. oldal		PDF \| MathML
Témakör(ök):	Háromszög nevezetes körei, Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Szögfelező egyenes, Körülírt kör, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1938/február: 1409. matematika feladat

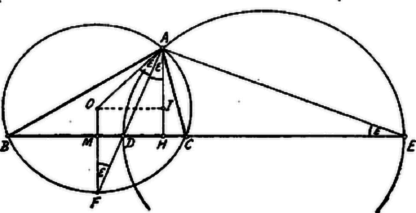
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az adatok közötti összefüggések vizsgálata céljából legyen $A B C △$ a keresett háromszög, az $α$ szög felezője $A D = l_{α}$ , az $A D$ -re merőleges külső szögfelező $A E$ ; a $B C$ oldalhoz tartozó Apollonius-kör átmérője $D E = 2 k_{α}$ . A körülírt kör középpontja $O$ , sugara $r = O A = O F$ , ahol $F$ a $\hat{B C}$ ív felezőpontja, amelyen keresztülmegy az $A D$ szögfelező.

A rövidség kedvéért legyen

A E D ∢ = ε

. Az

O F A ∢ = ε

, mert szárai megfelelően merőlegesek az

A E D

száraira. Mivel pedig

O F = O A

, az

O A F ∢ = O F A ∢ = ε

.
Ezek alapján a szerkesztést máris el tudjuk végezni. Kijelöljük az Appolloniuskör

D E = 2 k_{α}

, átmérőjét, megrajzoljuk ezen átmérőhöz tartozó kört és e körben felmérjük a

D A = l_{α}

hosszúságú húrt, hacsak

l_{α} < 2 k_{α}

Ezután

A D

-re az

A

csúcsnál rámérjük a

D A O ∢ = D E A ∢ = ε

szöget és ezen szög másik szárára felmérjük az

A O = r

távolságot. Az

O

pontból

O A = r

sugárral szerkesztett kör a

D E

egyenest a

B

és

C

csúcsokban metszi, hacsak az

O

pont távolsága a

D E

egyenestől, t. i.

O M < r

.
Az így nyert

A B C △

valóban megfelel a követelményeknek. Ugyanis, a szerkesztésből következik:

O F = O A

, tehát

O F A ∢ = O A F ∢ = ε

. Azonban

F A ⊥ A E

; kell tehát, hogy

O F ⊥ B C

legyen, azaz

F

felezi

\hat{B C}

ívet,

A F

ill.

A D

valóban felezi az

α

szöget és így

D E

B C

oldalhoz tartozó Apollonius-kör átmérője.
Már most vizsgáljuk meg közelebbről az

O M < r

feltételt. Legyen

A H ⊥ B C

és

O

vetülete az

A H

-n

I

; ekkor

O M = I H = A H - A I

.
Az

A D E

derékszögű háromszögű háromszögben

\begin{matrix} A H \cdot D E = A D \cdot A E azaz A H = \frac{A D \cdot A E}{D E} = \frac{l \cdot \sqrt[]{4 k^{2} - l^{2}}}{2 k} \end{matrix}

ahol egyelőre

k

és

l

indexét elhagytuk.
Az

O A I

derékszögű háromszögben

O A I ∢ = 2 ε

,^{$^{*}$}tehát

\begin{matrix} A I = O A cos 2 ε = r (1 - 2 sin^{2} ε) = r (1 - 2 \frac{l^{2}}{4 k^{2}}) . \end{matrix}

A szerkesztés lehetőségének feltétele:

\begin{matrix} \frac{l \sqrt[]{4 k^{2} - l^{2}}}{2 k} - r (1 - \frac{2 l^{2}}{4 k^{2}}) < r vagy \frac{l \sqrt[]{4 k^{2} - l^{2}}}{2 k} < \frac{2 r}{4 k^{2}} (4 k^{2} - l^{2}) . \end{matrix}

Egyszerűsítés és négyzetreemelés után

\begin{matrix} l^{2} < \frac{r^{2}}{k^{2}} (4 k^{2} - l^{2}), ill. l_{α}^{2} < \frac{4 k_{α}^{2} r^{2}}{k_{α}^{2} + r^{2}} . \end{matrix}

Ha ezen feltétel ki van elégítve, akkor egyszersmind

l_{α}^{2} < 4 k_{α}^{2}

azaz

l_{α} < 2 k_{α}

Sándor Gyula (Kölcsey Ferenc g. VII. o. Bp. VI.)

II. Megoldás. Kössük össze az Apollonius-kör

ω

középpontját a háromszög

A

csúcsával; ekkor

E A ω ∢ = ε

. Ha tehát az

E A D

derékszöget

A

körül

ε

szöggel elforgatjuk, akkor az

ω A O

szöget kapjuk, azaz

ω A O ∢ = 90^{\circ}

. Ez annyit jelent, hogy a háromszög köré irt

O

kör és bármely oldalhoz tartozó Apollonius-kör merőlegesen metszik egymást. Ennek alapján a szerkesztés így végezhető:

k_{α}

és

r

sugarakkal oly köröket szerkesztünk, melyek merőlegesen metszik egymást. A

k_{α}

sugarú körben felmérjük a két kör egyik metszéspontjából,

A

-ból az

A D = l_{α}

hosszúságú húrt (úgy, hogy az

O

körön is belül essék). Meghúzzuk az

ω D

egyenest; ez az

O

kört a

B

és

C

pontokban metszi és

A B C △

a keresett háromszög.
A szerkesztés lehetőségének feltétele, hogy

l_{α}

kisebb legyen a két kör közös húrjánál; ezen húr az

O A ω

derékszögű háromszög

O ω

átfogóhoz tartozó magasságának kétszerese. Az

O A ω △

befogói

k_{α}

r

, átfogója

\sqrt[]{k_{α}^{2} + r^{2}}

, az átfogóhoz tartozó magasság

\frac{k_{α} r}{\sqrt[]{k_{α}^{2} + r^{2}}}

. A szóbanforgó feltétel eszerint

\begin{matrix} l_{α} < \frac{2 k_{α} r}{\sqrt[]{k_{α}^{2} + r^{2}}} . \end{matrix}

Weisz Alfréd (Bólyai g. VIII. o. Bp.)

^{$^{*}$}T. i.

O A F ∢ = O F A ∢ = ε

és

F A I ∢ = O F A ∢

, mert

O F ∥ A H