Kezdőlap


Feladat:	1405. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Berger Tibor , Bulkay Lajos , Egri György , Freud Géza , Grosz László , Hoffmann Tibor , Hörcher J. , Komlós János , Krisztonosich Jenő , Mandl Béla , Nádor Gy. , Nagy Elemér , Sándor Gyula , Sauer Jenő , Schreiber Béla , Seidl Gábor , Taksony György [0-0]
Füzet:	1938/április, 242 - 244. oldal		PDF \| MathML
Témakör(ök):	Függvénytranszformációk, Egyenesek egyenlete, Parabola egyenlete, Kúpszeletek érintői, Pont, Parabola, mint kúpszelet, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1938/február: 1405. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $y^{2} = 2 p x$ parabola $(x_{0}; y_{0})$ pontjában húzott érintő irányhatározója: $\frac{p}{y_{0}}$ , tehát a normálisé: $- \frac{y_{0}}{p}$ . Az $M$ $(x_{0}, y_{0})$ ponthoz tartozó normális egyenlete:

\begin{matrix} y - y_{0} = - \frac{y_{0}}{p} (x - x_{0}) vagy y - y_{0} = - \frac{y_{0}}{p} (x - \frac{y_{0}^{2}}{2 p}) . \end{matrix}

Legyen

- \frac{y_{0}}{p} = m

, tehát

y_{0} = - p m

, azaz a normális egyenletébe az

y_{0}

paraméter helyett vezessük be a normális irányhatározóját paraméterként. Így a normális egyenlete

\begin{matrix} y + p m = m (x - \frac{p m^{2}}{2}) vagy y = m (x - p) - \frac{p m^{3}}{2} . \end{matrix}

Helyezzük a koordinátarendszer kezdőpontját a parabola gyújtópontjába, de a tengelyek iránya ugyanaz maradjon. Az új koordináták és ez eredetiek között

\begin{matrix} x' = x - \frac{p}{2}, y' = y, ill. x = x' + \frac{p}{2}, y' = y \end{matrix}

transzformációs kapcsolatok állanak fenn és így az új koordinátarendszerben a normális egyenlete

\begin{matrix} y' = m (x' - \frac{p}{2}) - \frac{p m^{3}}{2}, \end{matrix}

ill. a vesszős jelzést elhagyva,

\begin{matrix} y = m (x - \frac{p}{2}) - \frac{p m^{3}}{2} ... \end{matrix}

(1)

A gyújtóponton átmenő és a normálisra merőleges egyenes egyenlete:

\begin{matrix} y = - \frac{1}{m} x ... \end{matrix}

(2)

Az (1) és (2) egyenletekből álló rendszert megoldva, a két egyenes metszőpontjának koordinátáit kapjuk, mint

m

függvényeit. Ha pedig az

m

paramétert kiküszöböljük a két egyenletből, a metszéspont koordinátái között kapunk összefüggést, mely a keresett mértani hely egyenlete. (2)-ből

m = - \frac{x}{y}

. Ezt (1)-be helyettesítve:

\begin{matrix} y = - \frac{x}{y} (x - \frac{p}{2}) + \frac{p}{2} \frac{x^{3}}{y^{3}} vagy y^{4} + x^{2} y^{2} - \frac{p}{2} x y^{2} - \frac{p}{2} x^{3} = 0, \end{matrix}

ill.

\begin{matrix} y^{2} (y^{3} - \frac{p}{2} x) + x^{2} (y^{2} - \frac{p}{2} x) \equiv (x^{2} + y^{2}) (y^{2} - \frac{p}{2} x) = 0 ... \end{matrix}

(3)

A szóbanforgó mértani hely eszerint két részből áll: az egyik rész

x^{2} + y^{2} = 0

egyenletnek felel meg és ez nem más, mint maga a gyújtópont (ill. a gyújtóponton átmenő képzetes egyenespár). A másik rész az

y^{2} - \frac{p}{2} x = 0

egyenletnek megfelelő parabola, melynek csúcspontja az eredeti parabola gyújtópontja és paramétere

\frac{p}{4}

az eredeti paraboláénak negyedrésze.
Krisztonosich Jenő (Szent László g. VIII. o. Bp. X.).

II. Megoldás. Az előbbi eredményt szintétikus geometriai eljárással világítjuk meg. Legyen

I

F

gyújtópont vetülete az

M N

normálison. Minthogy

F M = F N

, az

I

felezi

M N

-t. Ha

M P

felezőpontja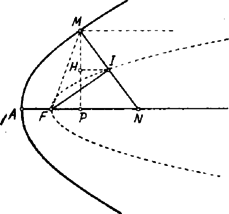

H

, akkor

H I ∥ P N

és

H I = \frac{1}{2}, P N = \frac{1}{2} p

A parabola pontjaihoz tartozó

(M P)

ordináták felezőpontjai azonban ugyancsak parabolát írnak le, melynek csúcsa az adott paraboláéval közös

(A)

és paramétere

\frac{p}{4}

. Ha ezen parabolát főtengelyével párhuzamosan eltoljuk és az eltolás mértéke

H I = \frac{p}{2}

, akkor megkapjuk az

I

pont mértani helyét, oly parabolát, melynek csúcsa

F

, paramétere

\frac{p}{4}

és tengelye az adott paraboláéval közös.

Sauer Jenő (Bencés g. VII. o. Győr.)