Kezdőlap


Feladat:	1402. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Berger Tibor , Bizám György , Bulkay Lajos , Csimadia P. , Csuri Vilmos , Dónáth G. , Egri György , Faludi J. , Fekete András , Fonó András , Fonó Péter , Freud Géza , Halász Iván , Haraszthy András , Hódi Endre , Hoffmann Tibor , Hörcher J. , ifj. Jankovich I. , ifj. Schütz B. , ifj. Seidl Gábor , Kaiser K. , Koch Gy. , Komlós János , Kovács E. , Kovács L. , Krisztonosich Jenő , Laub György , Mandl Béla , Mészáros György , Nádor Gy. , Pfeifer Béla , Sándor Gyula , Schreiber Béla , Sulner László , Sydó Sándor , Szerényi László , Szittyai Dezső , Taksony György [0-0] , Tóth M. , Trunkó Gy.
Füzet:	1938/április, 239 - 241. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Irracionális egyenletek, Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Gyökös függvények, Feladat
Hivatkozás(ok):	Feladatok: 1938/február: 1402. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egyenletünk aequivalens a következő egyenletrendszerrel:

\begin{matrix} \sqrt[]{x + 1} = u, \sqrt[]{2 x + 1} = v, u - v = m, \end{matrix}

ill.

\begin{matrix} x + 1 = u^{2}, 2 x + 1 = v^{2}, u - v = m ... \end{matrix}

(1)

ahol

\begin{matrix} u > 0, v > 0. \end{matrix}

v

kiküszöbölésével:

\begin{matrix} v = u - m, x + 1 = u^{2}, 2 x + 1 = {(u - m)}^{2} ... \end{matrix}

(2)

vagy

\begin{matrix} v = u - m, x = u^{2} - 1, f (u) \equiv u^{2} + 2 m u - m^{2} - 1 = 0 ... \end{matrix}

(3)

ahol

\begin{matrix} u > 0 és u - m > 0, azaz u > m ... \end{matrix}

(4)

Meg kell oldanunk tehát a (3) egyenletet

u

-ra nézve, a (4) feltételek tekintetbe vételével.
I. Legyen

m < 0

. Ekkor, ha

u > 0

ki van elégítve,

u > m

. Ha azonban

m < 0

, akkor a (3) egyenletnek mindig van két valós gyöke, ellenkező előjellel; ezek között a pozitív

\begin{matrix} u = - m + \sqrt[]{2 m^{2} + 1} \end{matrix}

és így

\begin{matrix} x = u^{2} - 1 = 3 m^{2} - 2 m \sqrt[]{2 m^{2} + 1} . \end{matrix}

II.

m = 0

esetben (3)-ból:

\begin{matrix} f (u) = u^{2} - 1 = 0. \end{matrix}

Minthogy

\begin{matrix} u > 0, u = 1 és x = u^{2} - 1 = 0. \end{matrix}

III.

m > 0

. Most elegendő az

u > m

feltételt kielégíteni, mert ekkor

u > 0

. Minthogy a (3) egyenletnek valós gyökei vannak, ellenkező előjellel, csak az egyik: a pozitív felelhet meg, ha

m

-nél nagyobb.
Az

f (u)

u

oly másodfokú függvénye, mely a zérus helyek között negatív. A pozitív zérus hely nagyobb

m

-nél, ha

\begin{matrix} f (m) < 0, azaz 2 m^{2} - 1 < 0, tehát 0 < m < \frac{\sqrt[]{2}}{2} . \end{matrix}

Eszerint, ha

m

kielégíti ezen feltételt, akkor

\begin{matrix} u = - m + \sqrt[]{2 m^{2} + 1} és x = 3 m^{2} - 2 m \sqrt[]{2 m^{2} + 1} . \end{matrix}

Összefoglalva: ha

m

változik

- \infty

-től

+ \frac{\sqrt[]{2}}{2}

-ig, az egyenletnek egy megoldása van. Ha

m = \frac{\sqrt[]{2}}{2}

, akkor

x = - \frac{1}{2}

. Ha pedig

m > \frac{\sqrt[]{2}}{2}

, az egyenletnek nincs megoldása.

Freud Géza (Berzsenyi g. VI. o. Bp. V.)

Jegyzet: Vizsgáljuk az

\begin{matrix} y = \sqrt[]{x + 1} - \sqrt[]{2 x + 1} \end{matrix}

függvény változását. Valós értékeket csak akkor kapunk, ha

x \geq - \frac{1}{2}

, azaz a függvény értelmezési tartománya

x = - \frac{1}{2}

-től

x = + \infty

-ig terjed.
Ha

x = - \frac{1}{2}

y = \frac{\sqrt[]{2}}{2}

;

x = 0

helyen

y = 0

; ha

x = + \infty

y = - \infty

.
A függvény az előbb kijelölt intervallumban folytonos és állandóan fogy, mert differenciálhányadosa

\begin{matrix} y' = \frac{1}{2 \sqrt[]{x + 1}} - \frac{1}{\sqrt[]{2 x + 1}} < 0, ha csak x \geq - \frac{1}{2} . \end{matrix}

\begin{matrix} x = - \frac{1}{2} helyen y' = - \infty . \end{matrix}

Ábrázoljuk a következő két parabolának az

X

-tengely feletti részét:

\begin{matrix} a) y_{1} = \sqrt[]{x + 1}, b) y_{2} = \sqrt[]{2 x + 1} . \end{matrix}

Az a) alatti csúcsa az (

x = - 1

y = 0

) pont, a b) alattié

x = - \frac{1}{2}

y = 0

. A két parabolaág az

x = 0

y = 1

pontban metszi egymást.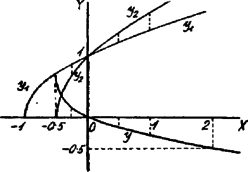

Ha az a) alatti parabola pontjaihoz tartozó ordinátákból kivonjuk a b) alatti parabola megfelelő pontjainak ordinátáit és ezen különbségeket az

X

-tengelyre merőlegesen felmérjük (a megfelelő

x

-helyen), az így nyert ordináták végpontjai az

\begin{matrix} y = \sqrt[]{x + 1} - \sqrt[]{2 x + 1} \end{matrix}

görbét adják.
Ezen görbe pontjaihoz tartozó ordináták

\frac{\sqrt[]{2}}{2}

-től 0-ig, azután 0-tól

- \infty

-ig változnak.
Ha az

X

-tengellyel

y = m

párhuzamos egyenest húzunk, akkor ezen egyenes a görbét egy- és csakis egy pontban metszi, hacsak

0 \leq m \leq \frac{\sqrt[]{2}}{2}

, ill.

m < 0