Kezdőlap


Feladat:	1397. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bolgár Imre , Bulkay Lajos , Csuri Vilmos , Fehér György , Fonó Péter , Freud Géza , Gáspár Rezső , Holló György , Klein József , Komlós János , Nagy Elemér , Radovics György , Sándor Gyula , Schreiber Béla , Sebestyén Gyula , Seidl Gábor , Sydó Sándor , Szerényi László , Szittyai Dezső
Füzet:	1938/március, 216 - 218. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Súlypont, Körülírt kör középpontja, Beírt kör középpontja, A háromszögek nevezetes pontjai, Húrnégyszögek, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1938/január: 1397. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a keresett háromszög 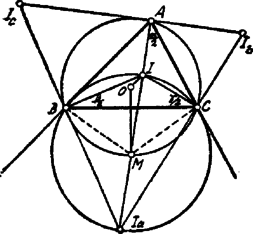$A B C △$ .
Az $I$ és $I_{a}$ középpontok az $A$ csúcsnál fekvő $α$ szöget felező egyenesen feküsznek. $I$ a belső szögfelezők közös pontja; $I_{a}$ az $α$ szöget, a $β$ és $γ$ mellékszögét felező egyenesek közös pontja, tehát $B I_{a} ⊥ B I$ és $C I_{a} ⊥ C I$ , azaz $B$ és $C$ az $I I_{a}$ átmérőjű körön feküsznek. Legyen ezen kör középpontja $M$ (az $I I_{a}$ távolság felezőpontja).

Kimutatjuk, hogy

M

A B C △

köré írt körön fekszik.
Ugyanis

\begin{matrix} B I C ∢ = 90^{\circ} + \frac{α}{2}, \end{matrix}

és így

\begin{matrix} B I_{a} C ∢ = 90^{\circ} - \frac{α}{2}, \end{matrix}

minthogy

I B I_{a} C

húrnégyszög az

I I_{a}

átmérőjű körben. Ezen körben a

B M C ∢

ugyanazon ívhez tartozó középponti szög, amelyhez a

B I_{a} C ∢

mint kerületi szög tartozik, tehát

\begin{matrix} B M C ∢ = 2 B I_{a} C ∢ = 180^{\circ} - α . \end{matrix}

Ebből következik, hogy

M

A B C △

köré írt körön fekszik (felezi ezen kör

\hat{B C}

ívét), azaz

O M = O B = O C

.
Eszerint

B

és

C

I I_{a}

átmérőhöz tartozó körnek és az

O

középpontú,

O M

sugarú körnek a közös pontjai. Az

A

csúcs az

I I_{a}

egyenesnek és az utóbbi körnek (az

M

-en kívüli) második közös pontja. Ezek alapján a szerkesztés el is végezhető és az így nyert

A B C △

megfelel. Ugyanis: 1) az

O

és

M

középpontú körök közös húrja,

B C

, merőleges az

O M

centrálisra; tehát

M

O

kör

B C

ívének felezőpontja.
2)

A I I_{a}

keresztülmegy az

A B C △

köré írt kör

B C

ívének

M

felezőpontján, tehát

A I I_{a}

felezi az

α

szöget.
3)

I C

felezi a

B C A ∢ = γ

szöget. T. i.

M I = M C

és így

M I C ∢ = M C I ∢

. Másrészt²

\begin{matrix} M I C ∢ = \frac{α}{2} + A C I ∢, azaz A C I ∢ = M I C ∢ - \frac{α}{2} . \\ M C I ∢ = M C B ∢ + B C I ∢ = \frac{α}{2} + B C I ∢, azaz B C I ∢ = M C I ∢ - \frac{α}{2}; \end{matrix}

ezekből következik

A C I ∢ = B C I ∢

, azaz

C I

felezi a

γ

szöget. Eszerint

I

valóban a beírt kör, és mivel

C I_{a} ⊥ C I

I_{a}

a hozzáírt kör középpontja.
Vizsgáljuk még a szerkesztés lehetőségének feltételét! Az

O

I

I_{a}

pontok úgy helyezkednek el, hogy

I

a háromszög köré írt körön belül,

I_{a}

e körön kívül fekszik; azaz szükséges és elegendő, hogy

\begin{matrix} O I < O M < O I_{a} \end{matrix}

legyen. Rögzítsük az

I

I_{a}

pontokat és így az

M

pontot is; húzzuk meg azt az egyenest, mely az

I M

távolságot merőlegesen felezi. Akkor az

O

pontnak a sík azon részében kell feküdnie, amelyben az

I

van. Ekkor valóban

\begin{matrix} O I < O M < O I_{a}, \end{matrix}

és a két kör, t. i. az

O

és

M

középpontú körök tényleg metszik egymást.

Schreiber Béla (izr. g. VIII. o. Bp.)

II. Megoldás. Ismeretes, hogy valamely háromszög magasságvonalai a talpponti háromszög szögfelezői. Az

A B C △

a hozzátartozó

I_{a} I_{b} I_{c} △

-re nézve talpponti háromszög, mert

\begin{matrix} I_{a} A ⊥ I_{b} I_{c}, I_{b} B ⊥ I_{c} I_{a}, I_{c} C ⊥ I_{a} I_{b}, \end{matrix}

azaz

I_{a} A

I_{b} B

I_{c} C

I_{a} I_{b} I_{c} △

magasságvonalai és így

I

I_{a} I_{b} I_{c} △

magassági pontja. Az

A B C △

köré írt kör középpontja eszerint az

I_{a} I_{b} I_{c} △

-re nézve Feuerbach-körének középpontja. Vagyis: az

I_{a} I_{b} I_{c} △

-re nézve adva van egyik csúcsa, pl.

I_{a}

, magassági pontja,

I

, és Feuerbach-körének középpontja,

O

. Az

I O

egyenes az

I_{a} I_{b} I_{c} △

Euler-egyenese.
A Feuerbach-kör, mint már több ízben láttuk, keresztülmegy a magasságok azon szeletének felezőpontján, mely a csúcs és a magassági pont között van; a jelen esetben tehát az

I I_{a}

távolság

M

felezőpontján.
Ezen tulajdonságok alapján úgy az

I_{a} I_{b} I_{c} △

, mint az

A B C △

megszerkeszthető.

^*L. ezen évf. 6. számában, az 1223. gyakorlatot! (1938/2 167. old. ‐a szerk.)

²L. az 1223. gyakorlat II. megoldását.