|
| Feladat: |
1395. matematika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bálint Gy. , Berger Tibor , Bluszt Ernő , Bulkay Lajos , Csuri Vilmos , Danciger E. , Donáth Géza , Etelaky L. , Gáspár Rezső , Grosz L. , Jani K. , Jankovich I. , Kelemen I. , Klein József , Lőke Péter , Mandl Béla , Marosán Zoltán , Mihalik I. , Nádor Gy. , Nagy Elemér , Radovics György , Rappaport S. , Sándor Gyula , Schreiber Béla , Szabó Béla , Székely Z. , Szentmiklósi L. , Szerényi László , Törley D. , Zsoldos E. |
| Füzet: |
1938/április,
236. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Terület, felszín, Paralelogrammák, Négyszögek geometriája, Koszinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Feladat, Másodfokú (és arra visszavezethető) egyenletrendszerek |
| Hivatkozás(ok): | Feladatok: 1938/január: 1395. matematika feladat |
|
|
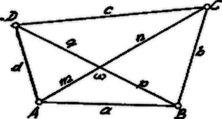
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A négyszög oldalai legyenek , , , , átlói és és ezek szöge (ill. ). Húzzunk a négyszög csúcsain keresztül a megfelelő átlókkal párhuzamosakat; az így keletkező parallelogramma oldalai és , ezek szöge , területe . A négyszög területe ennek fele: .
Az átlók szeletei legyenek ábránk szerint és , ill. és . A cosinustétel alkalmazásával:
Innen:
Az szorzat értékét utóbbi egyenletből kifejezzük és értékébe helyettesítjük. Így keletkezik: ahol az átlóknak azon szögét jelenti, amely az és oldalakkal fekszik szemben.
Donáth Géza (Áll. Szent László g. VIII. o. Bp. X.)
Jegyzet: Ha , akkor , ill. . Ebben az esetben a kifejezése nem ad határozott értéket. Képzeljünk egyszerűség kedvéért pl. egy rombust, megadott oldallal és a csúcsaiban csuklókkal ellátva. Az egyik oldalt rögzítjük, a többit forgatjuk; eközben az átlók mindig merőlegesek maradnak egymásra, a szembenfekvő oldalak négyzet összege mindig egyenlő egymással, azonban a területe változó. Jelölje a rombus oldalát : területe 0 és között változik.
Ha a tompaszög, akkor a vele szembenfekvő oldalak négyzetösszege: |
|
 PDF |
PDF |  MathML
MathML