| Feladat: | 1392. matematika feladat | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Berger Tibor , Csuri Vilmos , Fehér György , Freud Géza , Gállik István , Gáspár Rezső , Halász Iván , Kieweg Ferenc , Mandl Béla , Nagy Elemér , Sándor Gyula , Schreiber Béla , Sebestyén Gyula , Székely Z. , Szentmiklósi L. , Szerényi László | ||
| Füzet: | 1938/március, 211 - 212. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Elemi függvények differenciálhányadosai, Határozott integrál, Kör egyenlete, Kúpszeletek érintői, Terület, felszín, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1938/január: 1392. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ha a kör , pontjaiban az érintők párhuzamosak, akkor a kör átmérője és felezőpontja, t. i. az origo a kör középpontja, melynek egyenlete: A kör keresztülmegy a ponton; tehát: Eszerint a szóbanforgó kör:
Az inflexiós pont abscissája, amint az 1341. feladatban láttuk: . Most , tehát . Minthogy a görbe keresztülmegy az origón, a (2) egyenletet kielégíti és így . Eszerint a görbe egyenlete:
A görbe keresztülmegy a ponton, tehát
A görbének és a körnek közös érintőjük van az , pontokban. A kör érintőjének irányhatározója az pontban: , mert sugár iránytangense: . Ezért a (3) alatti , ha , vagyis
Keressük már most az (1) kör és a (6) görbe közös pontjait. Meg kell oldanunk az (1) és (6) egyenletekből álló rendszert. Ebből -t kiküszöböljük, ha a (6) alatti kifejezését (1)-be helyettesítjük:
Ezen egyenletnek és kétszeres gyökei ‐ az érintkezés miatt ‐ tehát kell, hogy az egyenlet baloldala osztható legyen A parabola és a kör metszéspontjai az egyenlet gyökeihez tartoznak: , . Ezen pontok az abscissa-tengelyen feküsznek. 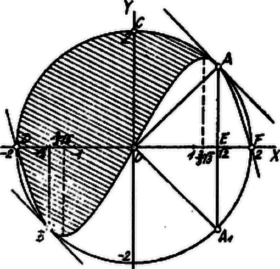 A két görbe által határolt terület nagyságát, és határok között a szimmetriából kifolyólag úgy kaphatjuk meg, hogy a kör területeiből kivonjuk a két görbének és közötti íveik által bezárt sarló alakú idom területének kétszeresét és az így nyert különbség fele adja meg a keresett terület nagyságát. Már most az húr a körben oly szeletet ‐ ‐ határoz meg, mely egy -ú körcikkből van lehasítva. A körcikk területe: . Az területe: . Így a körszelet területe: és ennek fele, az vegyesvonalú idomé ( a kör íve): . Ebből ki kell vonnunk az , és a parabola íve által határolt területet; minthogy és , Kieweg Ferenc (Kegyesrendi g. VIII. o., Bp.) |