Kezdőlap


Feladat:	1389. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Berger Tibor , Bizám György , Csuri Vilmos , Danciger E. , Egri György , Etelaky L. , Fehér György , Freud Géza , Gállik István , Gáspár Rezső , Gerő B. , Grosz L. , Hajnal Miklós , Halász Iván , Hoffmann Tibor , Hörcher J. , Jankovich István , Klein József , Komlós János , Mandl Béla , Mihalik I. , Nagy Elemér , Orosz Gy. , Pálfay Ferenc , Radovics György , Sándor Gyula , Schläffer Ödön , Schreiber Béla , Sebestyén Gyula , Sebők László , Seidl Gábor , Szabó Béla , Székely Z. , Szél Gy. , Szentmiklósi L. , Szerényi László
Füzet:	1938/március, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Terület, felszín, Geometriai valószínűség, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1938/január: 1389. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A négyzet $A$ , $B$ , $C$ , $D$ csúcsaiból szerkesszünk $a$ sugarú köröket; $a$ a négyzet oldala. E négy kör a négyzeten belül fekvő $A' B' C' D'$ görbevonalú négyszöget határozza meg. Ezen négyszöget határoló ívek mindegyike az $a$ sugarú kör kerületének $1 / 12$ -ed része. (Ugyanis az $a$ sugarú köröknek a négyzeten belül eső ívei 3 egyenlő részre osztják egymást.) Az $A' B' C' D'$ négyszög két átlója, $A' C'$ és $B' D'$ az $O$ pontban, a négyzet középpontjában metszi egymást és az $A' B' C' D'$ négyszöget négy egyenlő részre osztja.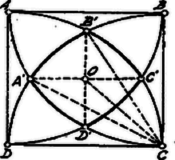

Egy ilyen rész, pl.

A' O B'

területét megkapjuk, ha az

A' C B'

körcikk területéből kivonjuk az

A' C O △

és

B' C O △

területének összegét, ill. az

A' C O △

kétszeres területét. Az

A' C B'

körcikk területe:

\frac{a^{2} π}{12}

.
Az

A' C O △

területe:

\begin{matrix} \frac{1}{2} A' C \cdot O C \cdot sin \hat{A' C O}^{1} = \frac{1}{2} a \cdot \frac{a \sqrt[]{2}}{2} sin \frac{π}{12} . \end{matrix}

¹
Az

A' O B'

idom területe:

\begin{matrix} \frac{a^{2} π}{12} - \frac{a^{2} \sqrt[]{2}}{2} sin \frac{π}{12} . \end{matrix}

A' B' C' D'

idom területe

4 A' O B' = a^{2} (\frac{π}{3} - 2 \sqrt[]{2} sin \frac{π}{12})

.
A feladatnak megfelelő pont ezen

A' B' C' D'

idomon belül, ill. ezen idom kerületén tartozik lenni. Annak valószínűsége, hogy a találomra felvett pont ne essék az

A' B' C' D'

zárt idomon kívül,

\begin{matrix} v = \frac{A' B' C' D'}{A B C D} = \frac{π}{3} - 2 \sqrt[]{2} sin \frac{π}{12} . \end{matrix}

Már most

\begin{matrix} sin \frac{π}{12} & = \sqrt[]{\frac{1 - cos \frac{π}{6}}{2}} = \frac{1}{2} \sqrt[]{2 - \sqrt[]{3}} \\ 2 \sqrt[]{2} sin \frac{π}{12} & = 2 \sqrt[]{2} \cdot \frac{1}{2} \sqrt[]{2 - \sqrt[]{3}} = \sqrt[]{4 - 2 \sqrt[]{3}} = \sqrt[]{3 - 2 \sqrt[]{3} + 1} = \\ = \sqrt[]{{(\sqrt[]{3} - 1)}^{2}} = \sqrt[]{3} - 1 \end{matrix}

és így

\begin{matrix} v = \frac{π}{3} - (\sqrt[]{3} - 1) = \frac{π}{3} + 1 - \sqrt[]{3} = 2, 0472 - 1, 7321 \\ v = 0, 3151 \end{matrix}

Jankovich István (érseki g. VIII. o. Bp. II.)

\hat{A' C O} = \frac{1}{2} \hat{A' C B'} = \frac{1}{2} \cdot \frac{2 π}{12} = \frac{π}{12}