Kezdőlap


Feladat:	1386. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Sándor Gyula
Füzet:	1938/február, 180 - 181. oldal		PDF \| MathML
Témakör(ök):	Paralelepipedon, Magasságvonal, Köréírt alakzatok, Mértani helyek, Rombuszok, Térgeometriai bizonyítások, Tetraéder magasságpontja, Feladat
Hivatkozás(ok):	Feladatok: 1937/december: 1386. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az orthocentrikus tetraéder legyen $A_{1} A_{2} A_{3} A_{4}$ ; a köréje írt parallelepipedon élei egyenlők, határlapjai rombuszok. Ezen tetraéder szemközti élei merőlegesek egymásra, pl. $A_{1} A_{2} ⊥ A_{3} A_{4}$ . (Az $A_{3} A_{4}$ él párhuzamos az $A_{1} B_{2} A_{2} B_{1}$ határlap $B_{3} B_{4}$ átlójával.)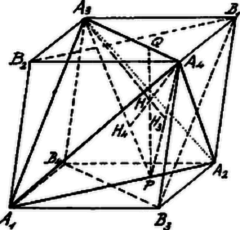

A_{3} A_{4}

élen keresztül fektessünk síkot, mely merőleges

A_{1} A_{2}

-re és

A_{1} A_{2}

-t a

P

-ben metszi;

P

-ből állítsunk merőlegest

A_{3} A_{4}

-re,

P Q

-t. Ekkor

P Q

A_{1} A_{2}

és

A_{3} A_{4}

élek normáltranszverzálisa és az

A_{3} A_{4} P △

-ben az

A_{3} A_{4}

oldalhoz tartozó magasság.
Minthogy

A_{1} A_{2} ⊥ [A_{3} A_{4} P]

A_{1} A_{2} ⊥ A_{3} P

és

A_{1} A_{2} ⊥ A_{4} P

. Ez annyit jelent, hogy

A_{3} P

A_{1} A_{2} A_{3} △

A_{4} P

A_{1} A_{2} A_{4} △

egyik magassági vonala.
Az orthocentrikus tetraéderben a tetraédermagasságok talppontjai a megfelelő határháromszög magassági pontjai. Eszerint az

A_{4}

csúcsból kiinduló

m_{4}

magassági vonal

H_{4}

talppontja

A_{3} P

-n, az

A_{3}

csúcsból kiinduló

m_{3}

-é,

H_{3}

, az

A_{4} P

-n fekszik.

m_{3}

és

m_{4}

A_{3} A_{4} P △

-nek is magasságvonalai. Ezek azonban a tetraéder

H

magassági pontjában metszik egymást, tehát

H

A_{3} A_{4} P △

-nek is magassági pontja: ezen keresztül kell mennie a háromszög harmadik magassági vonalának, t. i.

P Q

-nak is.

II. Megoldás. Az egyenlő élű parallelepipedon

A_{1}

A_{2}

A_{3}

A_{4}

csúcsai az

A

, a többi

B_{1}

B_{2}

B_{3}

B_{4}

csúcsai a

B

tetraédert határozzák meg; mind a kettő orthocentrikus. Az

A

tetraéder

H

magassági pontja a

B

tetraéder köré írt gömb középpontja, tehát

H B_{1} = H B_{2} = H B_{3} = H B_{4}

. Tekintsük már most pl. az

A_{1} A_{2}

és

A_{3} A_{4}

szembenfekvő (egymásra merőleges) élek transzverzálisát,

P Q

-t. Ez, amint előbb láttuk, benn van az

A_{3} A_{4}

élen átfektetett

Σ

síkban, mely

A_{1} A_{2}

-re merőleges. Ezen

Σ

sík merőleges a

B_{1} B_{2}

egyenesre és a

B_{1} B_{2}

-t merőlegesen felező

A_{3} A_{4}

-n megy keresztül, tehát mértani helye mindazon pontoknak, amelyek

B_{1}

-től és

B_{2}

-től egyenlő távolságban vannak. De

P Q

benne van azon

Σ'

síkban is, melyet az

A_{1} A_{2}

élen átfektetünk

A_{3} A_{4}

-re merőlegesen;

Σ'

mértani helye eszerint azon pontoknak, amelyek

B_{3}

-tól és

B_{4}

-től vannak egyenlő távolságban. Tehát

P Q

bármely pontja egyenlő távolságban van egyrészt

B_{1}

- és

B_{2}

-, másrészt a

B_{3}

- és

B_{4}

csúcsoktól. Most még azt kell kimutatnunk, hogy

P Q

-nak van oly pontja, mely valamennyi

B

csúcstól egyenlő távolságban van.
Fektessünk az

A_{2} A_{4}

élen keresztül síkot, mely

A_{1} A_{3}

-ra merőleges. Ezen sík,

Σ''

, mértani helye mindazon pontoknak, melyek

B_{1}

-től és

B_{3}

-tól egyenlő távolságban vannak;

Σ''

P Q

-t egy oly

H

pontban metszi, melyre nézve

H B_{1} = H B_{3}

. Azonban az előbbiek szerint

H B_{2} = H B_{1}

és

H B_{4} = H B_{3}

és így

\begin{matrix} H B_{1} = H B_{2} = H B_{3} = H B_{4} . \end{matrix}

Eszerint

H

B

tetraéder köré írt gömb középpontja, ill. az

A

tetraéder magassági pontja, amelyen az

A

tetraéder szembenfekvő éleihez tartozó transzverzálisok bármelyike keresztül megy.