Kezdőlap


Feladat:	1384. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berger Tibor , Egri György , Freud Géza , Hoffmann Tibor , Holzer Pál , Hörcher János , Kemény György , Klein József , Sándor Gyula , Weisz Alfréd
Füzet:	1938/február, 179. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Szögfelező egyenes, Feuerbach-kör, Magasságpont, Paralelogrammák, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1937/december: 1384. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$A' B' C' △$ az $A B C △$ talpponti háromszöge. Erre nézve ismeretes: az $A B C △$ magasságai a talpponti háromszög szögfelezői; a talpponti háromszög szögei: 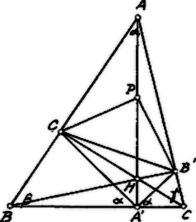$180^{\circ} - 2 α$ , $180^{\circ} - 2 β$ , $180^{\circ} - 2 γ$ .
Tudjuk továbbá azt is, hogy a háromszög Feuerbach-köre keresztül megy a talpponti háromszög csúcsain, továbbá az $A H$ $(B H$ , $C H)$ szelet felezőpontján.

A követelmény már most az, hogy a Feuerbach-körbe írt

A' B' P C'

négyszög parallelogramma legyen. Húrnégyszög parallelogramma csak a téglalap! Kell tehát, hogy

\begin{matrix} B' A' C ∢ = 180^{\circ} 2 α = 90^{\circ}, vagyis α = 45^{\circ} \end{matrix}

legyen. Ezen téglalapban az

A' P

átló felezi a

B' A' C' ∢

-et: ebből következik, hogy a téglalap négyzet; a másik átló

B' C' ⊥ P A

, azaz

B'

és

C'

A A'

-re nézve szimmetrikusan feküsznek. Ebből következik, hogy az

A B C △

egyenlőszárú, amelyben

\begin{matrix} β = γ = \frac{180^{\circ} - 45^{\circ}}{2} = 67^{\circ} 30' . \end{matrix}

Hoffmann Tibor (Szent István g. VI. o. Bp.)