Feladat: 1381. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Egri György ,  Freud Géza ,  Komlós János ,  Sándor Gyula ,  Somogyi Antal 
Füzet: 1938/február, 176 - 177. oldal  PDF  |  MathML 
Témakör(ök): Körérintők, Menelaosz-tétel, Egyenes, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1937/december: 1381. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Azon P pontok mértani helye, amelyekre nézve

AP:BP=m:n
oly kör, melynek középpontja az AB egyenesen van és az AB egyenest két pontban metszi (C és D) úgy, hogy
AC:CB=m:nésAD:BD=m:n.
A C pont A és B között van, a D az AB távolságon kívül.
Ha mn=p>1, akkor a szóbanforgó kör középpontja, I, az AB egyenesen, az AB-n kívül, a B felőli oldalon van, más szóval: B e körön belül, A e körön kívül fekszik és ekkor lehet A-ból a körhöz érintőt húzni.
Ha p=1, a körből egyenes lesz, mely AB-t merőlegesen felezi: C az O-ba, D a végtelenbe kerül.
(Ha p=∞, a kör a B pontba zsugorodik össze.
Ha o≤p<1, akkor az előbbi körökkel az O pontra nézve szimmetrikus köröket kapjuk; az A pont ezeken belül fekszik és a B-ből húzhatunk e körökhöz érintőket. Elegendő tehát, ha a p≥1 értékekhez tartozó köröket nézzük).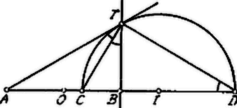
 
 

Egy tetszőleges körhöz, amelyre nézve p>1, az A pontból húzott érintő érintési pontja legyen T. Ekkor TC az ABT△ T csúcsához tartozó belső, TD pedig külső szögfelező és így TC⊥TD. Az ATC és TDC szögek, ‐ a CD átmérőjű körben a TC ívhez tartozó kerületi szögek ‐ egyenlők. Így
CTB∢=ATC∢=TDC∢

és, mivel iTDC∢+TCD∢=90∘,
azért CTB∢+TCB∢=90∘,
tehát TBC∢=90∘,
azaz a T érintési pont vetülete az AB egyesen mindig B, és így T az AB egyenesre, a B ponton állított merőlegesen fekszik. Minthogy T leírja egészen ezen egyenest, ‐ hacsak p≥1 ‐, a T pont mértani helye azon egyenes, mely AB-re a B pontban merőleges.
 
Somogyi Antal (gyakorló g. VIII. o. Bp.).