Feladat: 1378. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Berger Tibor ,  Bizám György ,  Bulkay Lajos ,  Büchler Magda ,  Csáky Gy. ,  Cseh Sándor ,  Csuri Vilmos ,  Egri J. ,  Fehér György ,  Freud Géza ,  Grünfeld Sándor ,  Halász Iván ,  Hibbey Levente ,  Hoffmann Tibor ,  Holzer Pál ,  ifj. Jankovich I. ,  ifj. Seidl Gábor ,  Komlós János ,  Mandl Béla ,  Nagy Elemér ,  Radovics György ,  Rigó Béla ,  Sándor Gyula ,  Sebestyén Gyula ,  Sommer György ,  Somogyi Antal ,  Szerényi László ,  Tőkés Anna 
Füzet: 1938/február, 173 - 174. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Mértani középtételek derékszögű háromszögekben, Trapézok, Síkgeometriai számítások trigonometria nélkül, Feladat, Esetvizsgálat
Hivatkozás(ok):Feladatok: 1937/december: 1378. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha MM' felezőpontja I, akkor MM'=2MI=2OP=2x. Az AMA' derékszögű háromszögből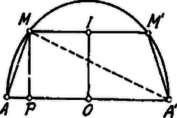

AM¯2=AA'¯⋅AP¯=AA'¯(OA-OP)=2r(r-x).

 

Minthogy M'A'=AM, feltételi egyenletünk
22r(2r-x)+2x=2lill.2r(r-x)=l-x
alakban írható. Ebből láthatjuk, hogy x≤l és x<r tartozik lenni és jelentésénél fogva pozitív.
Négyzetre emelve: 2r(r-x)=(l-x)2
ill. f(x)≡x2-2(l-r)x+l2-2r2=0.
mmmmmmmmmmmmmx=l-r±r(3r-2l).
Vizsgáljuk meg, hogy milyen feltételek mellett van elfogadható megoldás és hány van?
A gyökök valósak, ha l≤3r2.
f(r)=(l-r)2>0. Ebből következik, hogy r mindig a gyökökön kívül fekszik, még pedig nagyobb a gyököknél, mert nagyobb a gyökök félösszegénél, (l-r)-nél. Valóban
r>l-r,mert2r>l,  hacsak  l≤3r2.

f(l)=2r(l-r)>0, ha l>r. Ekkor l nagyobb a gyököknél, mert l>l-r, r>0. Ha l<r, akkor f(l)<0, tehát l a gyökök között van. Utóbbi esetben az egyik gyök negatív, a pozitív gyök pedig l-nél nagyobb: egyik sem felelhet meg.
f(0)=l2-2r2>0, ha l>r2. Ezen értékek mellett úgy a gyökök szorzata, mint a gyökök összege pozitív, tehát mindkét gyök pozitív és mindegyik kisebb l-nél (l>r!). Ha l<r2, akkor az egyik gyök negatív; a másik pozitív és kisebb l-nél mindaddig, amíg l>r.
Eszerint,
ha  r2<l<3r2,  két megoldás;ha  r<l<r2,  egy megoldás van;ha  l<r,  nincs megoldás.

Nézzük a határeseteket. Ha l=r, akkor x1=x2=r; a trapéz az AA' átmérőbe zsugorodik.
l=r2esetbenx1=0,x2=2r(2-1)∼0,83r.

l=3r2 mellett x1=x2=r2. Ekkor a trapéz a szabályos hatszög fele!
(AM=MM'=M'A'=r).
 
Halász Iván (Berzsenyi Dániel g. VII. o. Bp. V.)