Kezdőlap


Feladat:	1374. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1938/február, 182 - 184. oldal		PDF \| MathML
Témakör(ök):	Analógia, mint megoldási módszer, Terület, felszín, Térgeometriai bizonyítások, Térgeometriai számítások trigonometria nélkül, Tetraéder magasságpontja, Feladat
Hivatkozás(ok):	Feladatok: 1937/november: 1374. matematika feladat

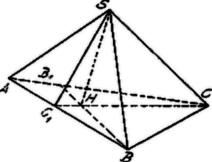
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Induljunk ki abból az esetből, amidőn a tetraéder $S$ csúcsában három, páronként egymásra merőleges él fut össze. Ilyenkor $S$ a tetraéder magassági pontja, az $S$ csúccsal szembenfekvő lapon $A B C △$ hegyesszögű háromszög tartozik lenni, ^{$^{*}$} az $S$ csúcsból az $A B C$ lapra bocsátott magasság talppontja az $A B C △$ magassági pontja. Az $A B C △$ területének négyzete pedig egyenlő az oldallapok ( $S A B$ , $S B C$ , $S C A$ ) területének négyzetösszegével. ^{$^{*}$}
Ha az $A B C △$ magassági pontja $H$ , az $A B C △$ magasságainak talppontjai (a háromszög megfelelő oldalain) $A_{1}$ , $B_{1}$ , $C_{1}$ , akkor, mivel $S A A_{1}$ , $S B B_{1}$ , $S C C_{1}$ az $S$ -nél derékszögű háromszögek,

\begin{matrix} {\bar{S H}}^{2} = \bar{A H} \cdot {\bar{H A}}_{1} = \bar{B H} \cdot {\bar{H B}}_{1} = \bar{C H} \cdot {\bar{H C}}_{1} \end{matrix}

és

\begin{matrix} {\bar{S A}}_{1}^{2} = \bar{A_{1} A} \cdot \bar{A_{1} H}, {\bar{S B}}_{1}^{2} = \bar{B_{1} B} \cdot \bar{B_{1} H} \\ {\bar{S C}}_{1}^{2} = \bar{C_{1} C} \cdot \bar{C_{1} H} . \end{matrix}

Megjegyezzük még, hogy az

S

csúcs az

A B C

síkra, a

H

pontban állított merőlegesnek és az

A B C △

bármely oldalához, mint átmérőhöz tartozó gömb metszéspontja. (L. a 466. feladatban!)
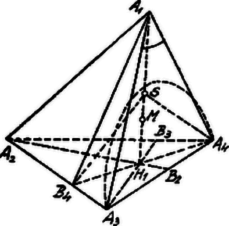
b) Legyen már most, az

A_{1} A_{2} A_{3} A_{4}

oly orthocentrikus tetraéder, melynek minden határlapja hegyesszögű háromszög, tehát mindegyik testszöglete hegyes.
Az orthocentrikus tetraéderben mindegyik magasság talppontja a szembenfekvő határlapon, az illető határlap ill. határháromszög magassági pontja ‐ hiszen az ilyen tetraéder szembenfekvő élei egymásra merőlegesek. (L. egyébként a II. évf. 179. oldalán a 110. feladatot!) Hegyesszögű háromszögben a magassági pont a háromszögön belül van; kell tehát, hogy a tetraéder magassági pontja a tetraéderen belül legyen.

Tekintsük pl. a tetraéder

A_{1} H_{1}

magasságát, ahol

H_{1}

A_{2} A_{3} A_{4} △

magassági pontja. Már most pl. az

A_{3} A_{4}

élhez, mint átmérőhöz tartozó gömb az

A_{1} A_{3} A_{4}

lapot egy legnagyobb körben metszi úgy, hogy

A_{1}

ezen körön, ill. a gömbön kívül fekszik; ^{$^{*}$} a gömb az

A_{1} H_{1}

magasságot oly

S

pontban metszi, mely

A_{1}

és

H_{1}

között fekszik és az

S A_{2} A_{3}

A_{4}

tetraéder az a) alatti tulajdonságokkal bír, úgy hogy

\begin{matrix} \bar{A_{1} H_{1}^{2}} > \bar{S H_{1}^{2}} = \bar{A_{i} H_{1}} \cdot \bar{H_{1} B_{i}} és \bar{A_{1} B_{i}^{2}} > S B_{i}^{2} = \bar{B_{i} A_{i}} \cdot \bar{B_{i} H_{1}} \end{matrix}

ahol

B_{i}

A_{2} A_{3} A_{1} △

A_{i}

csúcsából kiinduló magasság talppontja

(i = 2

3

4)

.
Eszerint

\begin{matrix} \bar{A_{1} B_{2}^{2}} > \bar{B_{2} A_{2}} \cdot \bar{B_{2} H_{1}} vagy {(\frac{1}{2} A_{1} B_{2} \cdot A_{3} A_{4})}^{2} > (\frac{1}{2} A_{3} A_{4} \cdot B_{2} A_{2}) (\frac{1}{2} A_{3} A_{4} \cdot B_{2} H_{1}) \\ \bar{A_{1} B_{3}^{2}} > \bar{B_{3} A_{3}} \cdot \bar{B_{3} H_{1}},, {(\frac{1}{2} A_{1} B_{3} \cdot A_{2} A_{4})}^{2} > (\frac{1}{2} A_{2} A_{4} \cdot B_{3} H_{3}) (\frac{1}{2} A_{2} A_{4} \cdot B_{3} H_{1}) \\ \bar{A_{1} B_{4}^{2}} > \bar{B_{4} A_{4}} \cdot \bar{B_{4} H_{1}},, {(\frac{1}{2} A_{1} B_{4} \cdot A_{2} A_{3})}^{2} > (\frac{1}{2} A_{2} A_{3} \cdot B_{4} A_{4}) (\frac{1}{2} A_{2} A_{3} \cdot B_{4} H_{1}) \end{matrix}

Az utóbbi egyenlőtlenségek azt fejezik, hogy mindegyik oldallap területe nagyobb, mint az alaplap és az oldallap (az alaplapon való) vetületének mértani középarányosa, ^{$^{*}$} azaz

\begin{matrix} t_{A_{1} A_{3} A_{4}}^{2} > t_{A_{2} A_{3} A_{4}} t_{A_{3} A_{4} H_{1}}, t_{A_{1} A_{2} A_{4}}^{2} > t_{A_{2} A_{3} A_{4}} \cdot t_{A_{2} A_{4} H_{1}}, \\ t_{A_{1} A_{2} A_{3}}^{2} > t_{A_{2} A_{3} A_{4}} \cdot t_{A_{2} A_{3} H_{1}} . \end{matrix}

Összeadva ezen egyenlőtlenségek megfelelő oldalait

\begin{matrix} t_{A_{1} A_{3} A_{4}}^{2} + t_{A_{1} A_{2} A_{4}}^{2} + t_{A_{1} A_{2} A_{3}}^{2} > t_{A_{2} A_{3} A_{4}} (t_{A_{3} A_{4} H_{1}} + t_{A_{2} A_{4} H_{1}} + t_{A_{2} A_{3} H_{1}}) . \end{matrix}

A jobboldali zárójeles összeg azonban az

A_{2} A_{3} A_{4} △

területét jelenti és így

\begin{matrix} t_{A_{2} A_{3} A_{4}}^{2} < t_{A_{1} A_{3} A_{4}}^{2} + t_{A_{1} A_{2} A_{4}}^{2} + t_{A_{1} A_{2} A_{3}}^{2} . \end{matrix}

Kimutattuk tehát, hogy ha az orthocentrikus tetraéder valamelyik testszöglete hegyes, akkor a szembenfekvő határlap területének négyzete kisebb, mint a többi lapokénak négyzetösszege!
c) Tegyük fel már most, hogy az

A_{1} A_{2} A_{3} A_{4}

orthocentrikus tetraéder olyan, hogy az

A_{1}

szöglet tompaszögű. Ekkor

A_{1}

-nek az alapélek bármelyikéhez, mint átmérőhöz tartozó gömb belsejében kell feküdnie ^{$^{*}$} és ekkor

A_{1} H_{1} < S H_{1}

(ahol

S

ugyanazt a pontot jelenti, mint b) alatt). A b) alatti egyenlőtlenségek értelme megváltozik, úgy hogy ezen esetben

\begin{matrix} t_{A_{2} A_{3} A_{4}}^{2} > t_{A_{1} A_{3} A_{4}}^{2} + t_{A_{1} A_{2} A_{4}}^{2} + t_{A_{1} A_{2} A_{3}}^{2}, \end{matrix}

azaz, ha a tetraéder egyik szöglete tompa, akkor az ezzel szembenfekvő határlap (területének) négyzete nagyobb, mint az oldallapok területének négyzetösszege.
Az ilyen tetraédernél a tetraéder magassági pontja a tetraéderen kívül esik. Ugyanis az

A_{i}

(i = 2

3

4)

csúcsból a szemközti határlapra bocsátott tetraédermagasság talppontja az illető határlap magassági pontja. Mivel pedig az

A_{i}

(i = 2

3

4)

csúccsal szembenfekvő határlap

A_{1}

-nél tompaszögű, ennek magassági pontja a háromszögön, ill. a tetraéderen kívül esik és így az

A_{i}

(i = 2, 3, 4)

csúcsokból kiinduló tetraéder-magasságok, ill. ezek metszőpontja, a tetraéder magassági pontja is a tetraéderen kívül esik.
Ezek alapján kell, hagy a feladatban foglalt tétel igaz legyen. Mert, ha mindegyik határlap (területének) négyzete kisebb a többi lapok négyzetösszegénél, akkor nem lehet, hogy az egyik szöglet derékszögű vagy tompaszögű legyen: az a) ill. c) eset állana elő a területek négyzetét illetőleg.
Ha pedig egyik határlap négyzete nagyobb a többiek négyzetösszegénél, akkor kell, hogy ezen határlappal szemben tompaszögű testszöglet legyen; mert ha nem az, akkor az a) vagy b) eset állana elő, a területek négyzetét illetőleg.

^{$^{*}$}L. V. évfolyamunk 241. oldalán a 466. feladatban (1929/4. 241. old. ‐ a szerk.)

^{$^{*}$}L. II. évfolyamunk 142. oldalán a 91. feladatban (1926/1. 142. old. ‐ a szerk.).

^{$^{*}$}Ugyanis $A_{3} A_{1} A_{4} ∢$ hegyesszög! A tetraéder $M$ magassági pontja $S$ és $H$ között fekszik. Ugyanis az $A_{1} A_{3} A_{4} △$ magassági pontja, $H_{2}$ , az $A_{3} A_{4}$ átmérő félkörön, ill. gömbön belül fekszik; ezen belül fekszik $S H_{1}$ is. ( $S$ a gömbön!) Így a tetraéder $A_{2} H_{2}$ magassága az $A_{1} H_{1}$ -et csak $S$ és $H_{1}$ között metszheti (az $M$ pontban).

^{$^{*}$}A $>$ jel helyett $=$ áll elő, ha $A_{1}$ -nél mindegyik élszög derékszög!

^{$^{*}$}Ha $A_{i} A_{1} A_{k} ∢ (i \neq k \pm 1)$ tompaszög, akkor $A_{1}$ az $A_{i} A_{k}$ átmérőjű körön belül fekszik!