Kezdőlap


Feladat:	1372. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bulkay Lajos , Füzy O. , Holzer Pál , Katter H. , Komlós János , Nagy Elemér , Rusznák I. , Seidl Gábor
Füzet:	1938/január, 153 - 154. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Komplex számok trigonometrikus alakja, Szabályos sokszögek geometriája, Vetítések, Feladat
Hivatkozás(ok):	Feladatok: 1937/november: 1372. matematika feladat

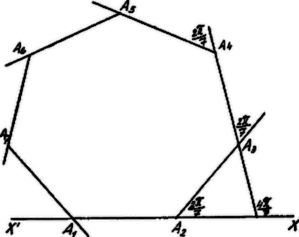
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Ha egy zárt sokszög oldalait, ugyanazon forgás irányban haladva, egy egyenesre vetítjük, a vetületek algebrai összege zérus.
Alkalmazzuk ezen tételt a szabályos hétszögre úgy, hogy az összes oldalakat az egyik oldalát tartó $X' X$ egyenesre vetítjük, a pozitív forgás irányában haladva.

A szabályos hétszög mindegyik szöge

π - \frac{2 π}{7}

.
Az első oldal és

X' X

egyenes hajlásszöge

0

; vetülete

a cos 0

. A következő oldal hajlásszöge

X' X

-hez

\frac{2 π}{7}

; vetülete

a cos \frac{2 π}{7}

. Minden következő oldal az előbbiből

\frac{2 π}{7}

mérőszámnak megfelelő szöggel fordul el, az

X' X

-hez való hajlásszög oldalról-oldalra haladva

\frac{2 π}{7}

-vel növekszik. Eszerint a vetületek összege:

\begin{matrix} x = a (cos 0 + cos \frac{2 π}{7} + cos \frac{4 π}{7} + cos \frac{6 π}{7} + cos \frac{8 π}{7} + cos \frac{10 π}{7} + cos \frac{12 π}{7}) = 0 ... \end{matrix}

(1)

Azonban

\begin{matrix} cos \frac{12 π}{7} - cos (2 π - \frac{12 π}{7}) = cos \frac{2 π}{7} . \end{matrix}

Hasonlóan

\begin{matrix} cos \frac{10 π}{7} = cos \frac{4 π}{7} és cos \frac{8 π}{7} = cos \frac{6 π}{7} . \end{matrix}

Eszerint a zárójelben foglalt összeg:

\begin{matrix} 1 + 2 (cos \frac{2 π}{7} + cos \frac{4 π}{7} + cos \frac{6 π}{7}) = 0, \\ cos \frac{2 π}{7} + cos \frac{4 π}{7} + cos \frac{6 π}{7} = - \frac{1}{2} . \end{matrix}

II. Megoldás. Az előbbi megoldásban kimutattuk, hogy

\begin{matrix} \sum_{k = 0}^{6} cos \frac{2 k π}{7} = cos 0 + cos \frac{2 π}{7} + cos \frac{4 π}{7} + cos \frac{6 π}{7} + cos \frac{8 π}{7} + cos \frac{10 π}{7} + cos \frac{12 π}{7} = 0. \end{matrix}

Ha figyelemmel vagyunk arra, hogy az

\begin{matrix} x^{7} - 1 = 0 \end{matrix}

egyenlet gyökei

\begin{matrix} cos \frac{2 k π}{7} + i sin \frac{2 k π}{7} (k = 0,1,2, ... 6) \end{matrix}

alakban írhatók és ezen gyökök összege zérus, akkor

\begin{matrix} \sum_{k = 0}^{6} cos \frac{2 k π}{7} = 0 és \sum_{k = 0}^{6} sin \frac{2 k π}{7} = 0. \end{matrix}

Komlós János (Gr. Széchenyi István gy. r. VIII. o. Pécs)
Nagy Elemér (Ciszterci Szent Imre g. VIII. o. Bp. XI.)

III. Megoldás. Vizsgáljuk az általánosabb

\begin{matrix} S = cos α + cos 2 α + cos 3 α + ... + cos n α \end{matrix}

(1)

összeget, amelyben a szögek számtani haladványt alkotnak; a haladvány első tagja

α

, különbsége is

α

^{$^{*}$}. Szorozzuk az 1) minden tagját

2 sin \frac{α}{2}

-vel. Ekkor

\begin{matrix} 2 cos α sin \frac{α}{2} = sin (α + \frac{α}{2}) - sin (α - \frac{α}{2}), \\ 2 cos 2 α sin \frac{α}{2} = sin (2 α + \frac{α}{2}) - sin (2 α - \frac{α}{2}), \\ 2 cos 3 α sin \frac{α}{2} = sin (3 α + \frac{α}{2}) - sin (3 α - \frac{α}{2}), \\ ... ... \\ 2 cos n α sin \frac{α}{2} = sin (n α + \frac{α}{2}) - sin (n α - \frac{α}{2}) . \end{matrix}

Minthogy

α + \frac{α}{2} = 2 α - \frac{α}{2}

2 α + \frac{α}{2} = 3 α - \frac{α}{2}

s. i. t, a jobboldalon álló tagok az összegezésnél eltűnnek, kivéve kettőt, úgyhogy

\begin{matrix} 2 S sin \frac{α}{2} = sin (n α + \frac{α}{2}) - sin (α - \frac{α}{2}) = 2 cos \frac{(n + 1) α}{2} sin \frac{n α}{2} . \end{matrix}

Az adott esetben

n = 3

α = \frac{2 π}{7}

, tehát

\begin{matrix} 2 S sin \frac{π}{7} = 2 cos \frac{4 π}{7} sin \frac{3 π}{7} = - 2 cos \frac{3 π}{7} sin \frac{3 π}{7} = - sin \frac{6 π}{7} . \end{matrix}

Azonban

\begin{matrix} sin \frac{6 π}{7} = sin (π - \frac{6 π}{7}) = sin \frac{π}{7}, \end{matrix}

és így

\begin{matrix} S = - \frac{1}{2} . \end{matrix}

^{$^{*}$}Az ilyen összeg kiszámítását tetszőleges különbség esetére is, lásd IV. évfolyamunk 197. o. (Goldziher: Goniometrikus többtagúak).