| Feladat: | 1361. matematika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Fehér György , Nagy Elemér , Sebestyén Gyula | ||
| Füzet: | 1937/december, 118 - 119. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Paralelepipedon, Súlyvonal, Négyszögek geometriája, Tetraéderek, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1937/október: 1361. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Megoldás. A parallelepipedon csúcsában összefutó élek: , , ; oldalátlók: , , ; testátlója . 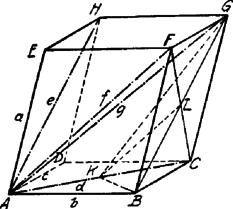 Kössük össze -t -vel és -vel. az -ben az oldalhoz tartozó súlyvonal. Ezért
A -ben pedig a oldalhoz tartozó súlyvonal és ezért:
Eszerint az általános parallelepipedonban az egy csúcsban ütköző élek és testátló négyzetének összege egyenlő az ugyanazon csúcsba ütköző három oldalátló négyzetének összegével. Jegyzet. Ezen tétel a matematikai irodalomban Euler‐féle tétel néven ismeretes. Érvényes a síknégyszögre abban az értelemben, amint ez a XIII. évf. 195. oldalán2, III. alatt látható: a síknégyszög oldalainak négyzetösszege egyenlő az átlók négyzetösszegével az átlók felezőpontjait összekötő távolság négyszeres négyzetével. II. Megoldás. IV. évfolyamunk 3. számában3 (54. o.), a 283. feladatban kimutattuk, hogy a parallelepipedon három, egy csúcsból kiinduló élének végpontjai oly háromszöget határoznak meg, melynek síkját a háromszög súlypontjában döfi át a szóbanforgó csúcsból kiinduló testátló, továbbá ezen pont a testátlót 1:2 arányban osztja két részre. Eszerint az tetraéderben a testátló része a tetraéder egyik súlyvonala, az súlypontján megy keresztül; az csúcsból kiinduló élek , , , az oldalai pedig az ,, oldalátlók. A tetraéderben pedig a testátló része azon súlyvonal, mely az súlypontján megy keresztül; a -ből kiinduló élek pedig a , , oldalátlókkal egyeznek meg. Alkalmazzuk már most ezen két tetraédernek -ból, ill. -ből kiinduló súlyvonalaira a 238. feladat keretében (III. évf. 243. o.4) kimutatott összefüggést a tetraéder egy‐egy súlyvonala és élei között; eszerint Fehér György (Fazekas Mihály r. VIII. o. Debrecen). Sebestyén Gyula (Fazekas Mihály r. VIII. o. Debrecen). 1Térnégyszög vagy torznégyszög.2az 1937. évi 3. számban (a szerk.)3az 1927. évi 10. számban (a szerk.)4az 1927. évi 4. számban (a szerk.) |