Kezdőlap


Feladat:	1360. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bagdy Dániel , Baskay I. , Bleyer J. , Cseresnyés Zoltán , Dudás Imre , Fehér György , Fekete András , Freud Géza , Halász Iván , Holzer Pál , Juhász Kató , Kemény György , Klein József , Komlós János , Nagy Elemér , Rappaport Sándor , Sándor Gyula , Schreiber Béla , Sebestyén Gyula , Steiner Iván , Sydó Sándor , Székely I. , Szilágyi S. , Than Károly , Tóbiás István , V. Nagy Sándor
Füzet:	1937/december, 117 - 118. oldal		PDF \| MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül körökben, Síkgeometriai szerkesztések, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1937/október: 1360. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $r$ sugarú $O$ kör mindazon $M M'$ húrjai, melyek $O$ -ból derékszög alatt láthatók, a körbe írt négyzet oldalával $(r \sqrt[]{2})$ egyenlők; ezen húrok távolsága $O$ -tól $\frac{1}{2} r \sqrt[]{2}$ , felezőpontjuk az $O$ körül $\frac{1}{2} r \sqrt[]{2}$ sugárral leírt $γ$ körön fekszik.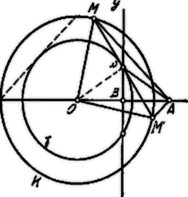

Legyen már most

M M'

egy ilyen húr, amely azonban

A

-ból is derékszög alatt látható. Így

M 0 M'

A

húrnégyszög oly körben, melynek középpontja

ω

; ez tehát

O

-tól és

A

-tól egyenlő távolságra lévén, az

O A

távolságot merőlegesen felező

B y

egyenesen fekszik.
Eszerint

ω

-t és így

M M'

-t is megkapjuk, ha megkeressük a

γ

körnek és az

O A

-t merőlegesen felező

B y

egyenes közös pontjait. Ilyen közös pont létezik, ha

O B ≦ O ω

, azaz, ha

O A = a

\begin{matrix} \frac{a}{2} ≦ \frac{1}{2} r \sqrt[]{2}, ill. a ≦ r \sqrt[]{2} . \end{matrix}

a < r \sqrt[]{2}

, két közös pont és így két megoldás van (

O A

-ra szimmetrikus helyzetben).

M M'

γ

kört

ω

-ban érinti

(M M' ⊥ O ω)

.
Ha

a = r \sqrt[]{2}

, egy közös pont és így egy megoldás van.

(M M' ⊥ O A)

.
Ha

a = 0

, azaz

A

és

O

összeesnek, végtelen sok megoldás van.

Schreiber Béla (izr. g. VIII. o. Bp.).

Jegyzet. Az

ω

pont az

O

-ból és

A

-ból

\frac{1}{2} r \sqrt[]{2}

sugárral rajzolt körök közös pontja.

O A

M A M' ∢

-et felezi, tehát

O A M ∢ = O A M' ∢ = 45^{\circ}

. A szerkesztés ezen alapon is végezhető.