Kezdőlap


Feladat:	1359. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baskay I. , Bleyer J. , Fehér György , Fekete András , Grosz László , Holzer Pál , Klein József , Komlós János , Laub Gy. , Laub György , Nagy Elemér , Papp István , Radovics György , Sándor Gyula , Schreiber Béla , Sebestyén Gyula , Sydó Sándor , Szegfü A. , Szittyai Dezső , Tóbiás István
Füzet:	1937/december, 115 - 117. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Szögfelező egyenes, Hozzáírt körök, Hossz, kerület, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1937/október: 1359. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A B C Δ$ a feltételeknek megfelelő. Hosszabbítsuk meg az $A B$ és $A C$ oldalakat, szerkesszük meg azon kört, mely az $α$ szög szárai között fekszik és a háromszöget kívülről érinti.¹ Ezen kör $I_{1}$ középpontja az $α$ -t felező egyenesen fekszik; ha érintési pontjai az oldalakon $A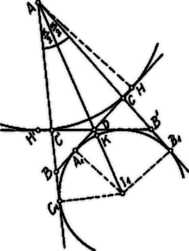_{1}$ , $B_{1}$ , $C_{1}$ , akkor

\begin{matrix} B A_{1} = B C_{1} és C A_{1} = C B_{1} . \end{matrix}

Minthogy

A B_{1} = A C_{1}

és

\begin{matrix} A B_{1} + A C_{1} = A C + C B_{1} + A B + B C_{1} = A C + A B + B C = 2 s, \end{matrix}

nyilván

\begin{matrix} A B_{1} = A C_{1} = s . \end{matrix}

B C

oldal az

A

középponttal bíró és

A H = m_{a}

sugarú körnek érintője, tehát közös belső érintője ezen és az

I_{1}

körnek.
A szerkesztés ezek alapján ez lesz. Az

α

szög száraira felmérjük a kerület felét:

A B_{1} = A C_{1} = s

távolságokat.

B_{1}

-ben ill.

C_{1}

-ben

A B_{1}

ill.

A C_{1}

-re merőlegest emelünk. Ez az

α

felezőjét

I_{1}

pontban metszi. Megrajzoljuk az

I_{1}

pontból az

I_{1} B_{1} = I_{1} C_{1}

sugarú és az

A

pontból az

A H

sugarú kört. E két kör közös belső érintője lesz a

B C

oldal tartója. (Két megoldás, az

α

felezőjére szimmetrikus helyzetben.)
Vizsgáljuk meg a szerkesztés lehetőségének feltételét. A határesetben ‐ t. i. amikor még van az előbb meghatározott két körnek közös belső érintője ‐ e két kör kívülről érinti egymást az

A I_{1}

szögfelező és az

I_{1}

kör

K

metszéspontjában. Kell tehát, hogy

A H = m_{a} < A K

legyen.
Már most

\begin{matrix} A K = A I_{1} - K I_{1} = \frac{A B_{1}}{cos \frac{α}{2}} - I_{1} B_{1} = \frac{s}{cos \frac{α}{2}} - s tg \frac{α}{2} = \frac{s}{cos \frac{α}{2}} (1 - sin \frac{α}{2}) . \end{matrix}

Eszerint a szerkesztés lehetőségének feltétele:

\begin{matrix} m_{a} < \frac{s (1 - sin \frac{α}{2})}{cos \frac{α}{2}} . \end{matrix}

II. Megoldás. A feltételeknek megtelelő

A B C Δ

B C

oldalát hosszabbítsuk meg mindkét irányban és mérjük fel rá a

B D = B A

és

C E = C A

távolságokat. Így egy olyan

A D E Δ

-et kaptunk, amely megszerkeszthető. Ugyanis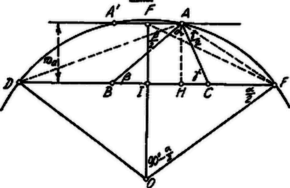

\begin{matrix} D E = D B + B C + C E = A B + B C + C A = 2 s . \end{matrix}

D E

oldalhoz tartozó magasság

A H = m_{a}

. Az

A B D Δ

egyenlőszárú; az

A D

alapján fekvő szögek összege

= β

, tehát mindegyikük

\frac{β}{2}

. Hasonlóan az

A C E Δ

-ben az

A E

alapon fekvö szögek mindegyike

\frac{γ}{2}

. Eszerint

\begin{matrix} D A E ∢ = α + \frac{β}{2} + \frac{γ}{2} = α + \frac{β + γ}{2} = α + 90^{\circ} - \frac{α}{2} = 90^{\circ} + \frac{α}{2} . \end{matrix}

A D E Δ

D E

oldala oly kör húrja, amelyhez tartozó nagyobbik kerületi szög

90^{\circ} + \frac{α}{2}

; a hozzátartozó domború középponti szög

180 + α

, tehát

D O E ∢ = 180^{\circ} - α

és a

D O E

egyenlőszárú háromszögben az alapon fekvő szögek mindegyike

\frac{α}{2}

A szerkesztés menete tehát ez lesz: tetszőleges egyenesen felmérjük a

D E = 2 s

távolságot (a szerkesztendő háromszög kerületét.) Ennek végpontjaiban

\frac{α}{2}

nagyságú szögeket mérünk fel úgy, hogy a

D O E

egyenlőszárú háromszög keletkezzék. Az

O D = O E

sugárral kört szerkesztünk; ennek kisebbik ívén kell az

A

csúcsnak feküdnie, a

D E

-től

m_{a}

távolságban.

D E

-re bárhol merőlegest emelünk, e merőlegesre felmérjük az

m_{a}

távolságot és ezen távolságban

D E

-vel párhuzamos

g

egyenest húzunk. Ahol

g

metszi az

O

kört, ott lesz a háromszög

A

csúcsa. Az

A D

ill.

A E

húrokat merőlegesen felező egyenesek

D E

-t a

B

ill.

C

csúcsban metszik.

g

egyenes az

O

kört két pontban metszi (

A

és

A'

); így 2 megoldást kapunk, az

O F (⊥ D E)

egyenesre szimmetrikus helyzetben: a két megoldás ugyanazon alkatrészekkel bíró háromszöget szolgáltat. Ha

g

érinti a kört, a két megoldás összeesik.

A

és

A'

F

-be esnek és

A B C Δ

egyenlőszárú lesz.
Hogy megoldás legyen, annak szükséges és elégséges feltétele, hogy

m_{a} ≦ F I

legyen, ahol

I

D E

felezőpontja.
Az

F I E

derékszögű háromszögben

I E = s

,
és

\begin{matrix} I F E ∢ = \frac{1}{2} D A E ∢ = \frac{1}{2} (90^{\circ} + \frac{α}{2}) = 45^{\circ} + \frac{α}{4} . \end{matrix}

Eszerint

F I = s cotg (45^{\circ} + \frac{α}{4})

.
A szerkesztés lehetőségének feltétele:

m_{a} < s cotg (45^{\circ} + \frac{α}{4})

Holzer Pál (Faludi Ferenc g. VIII. o. Szombathely.)

Jegyzet. A megoldás két feltételéből azt kell következtetnünk, hogy

\begin{matrix} \frac{1 - sin \frac{α}{2}}{cos \frac{α}{2}} = cotg (45^{\circ} + \frac{α}{4}) = tg (45^{\circ} - \frac{α}{4}) . \end{matrix}

Ennek kimutatásét az 1382. feladatban tűzzük ki.

¹A háromszöghöz hozzáírt kör!