Kezdőlap


Feladat:	1350. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fehér György , Grosz László , Holzer Pál , Jónás Emil , Nagy Elemér , Sebestyén Gyula , Sydó Sándor , Szabó János , Szerényi László , Szkitsák Rudolf
Füzet:	1937/november, 83 - 84. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Térfogat, Szélsőérték-feladatok differenciálszámítás nélkül, Tetraéderek, Feladat, Gömbi geometria
Hivatkozás(ok):	Feladatok: 1937/szeptember: 1350. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . A $P A B Q$ tetraéder alapjának tekintsük az $A$ -nál derékszögű $P A B$ háromszöget. Minthogy $B Q ⊥ B A$ és $B Q ⊥ A P$ , azért $B Q$ merőleges a $P A B$ síkra és így $B Q$ a $P A B$ alaphoz tartozó magasság. Eszerint a tetraéder térfogata

\begin{matrix} V = \frac{1}{2} A B \cdot A P \cdot \frac{1}{3} B Q = a \cdot x \cdot \frac{1}{3} y = \frac{1}{3} a x y = \frac{1}{3} a k^{2} \end{matrix}

azaz

V

értéke állandóan ugyanakkora.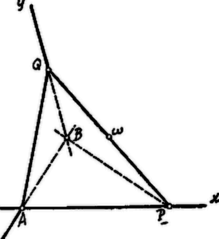

2^{0}

. Ha az

A

csúcs távolsága a

P B Q

laptól

h

, akkor

\begin{matrix} V = \frac{1}{3} h t_{P B Q} \end{matrix}

Láttuk, hogy

B Q ⊥ [P A B]

, tehát

B Q ⊥ B P

, azaz: a

P B Q Δ

B

-nél derékszögű és így

\begin{matrix} t_{P B Q} = \frac{1}{2} B Q \cdot B P = \frac{1}{2} y \sqrt[]{{\bar{A B}}^{2} + A P^{2}} = \frac{1}{2} y \sqrt[]{4 a^{2} + x^{2}} = \frac{1}{2} \sqrt[]{4 a^{2} y^{2} + k^{4}} . \\ V = \frac{1}{6} h \sqrt[]{4 a^{2} y^{2} + k^{4}}, innen h = \frac{6 V}{\sqrt[]{4 a^{2} y^{2} + k^{4}}} = \frac{2 a k^{2}}{\sqrt[]{4 a^{2} y^{2} + k^{4}}} . \end{matrix}

3^{0}

A P ⊥ A B

és

A P ⊥ B Q

, tehát

A P ⊥ [A B Q]

, ill.

A P ⊥ A Q

. Eszerint

P Q

közös átfogója a

B

-nél derékszögű

P B Q

és az

A

-nál derékszögű

P A Q

háromszögeknek. Ezért

P Q

felezőpontja

ω

, egyenlő távolságban van

P

Q

A

B

pontoktól, tehát a tetraéder köré írt gömb középpontja. E gömb átmérője

P Q

és

\begin{matrix} {\bar{P Q}}^{2} = {\bar{B P}}^{2} + {\bar{B Q}}^{2} = {\bar{A B}}^{2} + {\bar{A P}}^{2} + {\bar{B Q}}^{2} = 4 a^{2} + x^{2} + y^{2} = \\ = 4 a^{2} + {(x - y)}^{2} + 2 x y = 4 a^{2} + 2 k^{2} + {(x - y)}^{2} \end{matrix}

P Q

gömbátmérő minimum, ha

{(x - y)}^{2} = 0

, azaz, ha

x = y = k

Jónás Emil (Balassi Bálint g. VIII. o. Balassagyarmat)