Kezdőlap


Feladat:	1349. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berger Tibor , Fehér György , Holzer Pál , Mandl Béla , Nagy Elemér , Radovics G. , Schreiber Béla , Sebestyén Gyula
Füzet:	1937/november, 82 - 83. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Egyenes, Paralelogrammák, Szögfüggvények, síkgeometriai számítások, Mértani helyek, Feladat
Hivatkozás(ok):	Feladatok: 1937/szeptember: 1349. matematika feladat

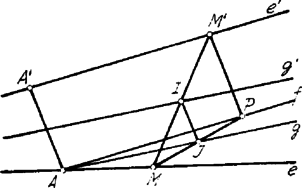
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $M'$ pontból húzzuk meg $M' P$ -t úgy, hogy $M' P # A' A$ legyen. (A párhuzamosság ugyanolyan irányú is legyen). Ekkor $A' M' P A$ parallelogramma, azaz $A P # A' M'$ , tehát a $P$ pont az $e'$ -vel párhuzamos és $A$ ponton átmenő $f$ egyenest írja le. Minthogy most $\frac{A M}{A P} = k$ , az $M P$ iránya mindig ugyanaz és így az $M P$ felezőpontja $J$ , az $A$ ponton átmenő $g$ egyenest írja le.

Legyen

I

M M'

felezőpontja, tehát

J I ∥ P M'

és

J I = \frac{1}{2} P M' = \frac{1}{2} A A'

.
Eszerint

J I

nagyságra nézve állandó, irányra nézve pedig

P M'

ill.

A A'

irányával egyezik meg. Tehát az

I

pont mértani helye azon

g'

egyenes, mely párhuzamos

g

-vel és

A A'

-t felezi.

Jegyzet. Néhány dolgozatban azon állítás, ill. következtetés foglaltatik, hogy az

I

pont mértani helye, a

g'

egyenes keresztülmegy az

e

és

e'

egyenesek

O

metszőpontján. Egyszerű meggondolás alapján mondhatjuk, hogy ez általában lehetetlen; ha ugyanis

O

valamely

M M'

távolság felezőpontja, akkor

M'

M O

egyenes mentén kell, hogy feküdjék, tehát

M'

is az

e

-nek pontja. Eszerint:

O

csak abban az esetben lehet az

I

mértani helyének pontja, ha

M

és

M'

összeesik az

O

-ban, azaz

k

oly értéke mellett, amellyel

\frac{A O}{A' O} = k

. (Ez a helyzet a

g

-re nézve!) Ekkor az összes

M M'

távolságok párhuzamosak!
Minthogy a beérkezett dolgozatok a feladatot analitikai úton tárgyalják, ilyen megoldást is közlünk.

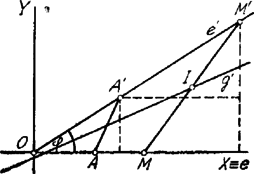
II. Megoldás. Derékszögű koordinátarendszerünk

X

tengelye legyen az

e

egyenes, kezdőpontja az

e

és

e'

egyenesek

O

metszőpontja. Az

e'

egyenes hajlásszöge az

X

tengelyhez legyen

φ

A

pont koordinátái: (

a

0

). Az

M

ponté: (

a + λ

0

), ahol

λ = A M

felvehet minden értéket

- \infty

-től

+ \infty

-ig.
Az

A'

pont koordinátái (

a'

a' tg φ

).
Minthogy

A' M' = \frac{A M}{k} = q \cdot A M^{} = q λ

,
az

M'

pont koordinátái:

(a' + q λ cos φ, a' tg φ + q λ sin φ)

. ^{$^{*}$} Az

M M'

távolság

I

felezőpontjának koordinátái:

\begin{matrix} ξ = \frac{a + λ + a' + q λ cos φ}{2}, η = \frac{a' tg φ + q λ sin φ}{2} . \end{matrix}

Amint látjuk, (

ξ

η

) a

λ

paraméter elsőfokú függvényei. Ha

λ = 0

ξ = \frac{a + a'}{2}

η = \frac{a' tg φ}{2}

. Ezen koordináták az

A A'

távolság felező pontját határozzák meg: ezen pont a mértani helyhez tartozik.
Hogy

ξ

és

η

között nyerjünk összefüggést,

λ

-t ki kell küszöbölnünk.
Írhatjuk:

\begin{matrix} 2 ξ - a - a' = λ (1 + q cos φ), 2 η - a' tg φ = λ q sin φ, \end{matrix}

tehát

\begin{matrix} \frac{2 η - a' tg φ}{2 ξ - a - a'} = \frac{q sin φ}{1 + q cos φ} ill. 2 η - a' tg φ = \frac{q sin φ}{1 + q cos φ} - (2 ξ - a - a') . \end{matrix}

Ha már most (

ξ

η

) helyett (

x

y

)-t írunk, a keresett mértani hely egyenlete:

\begin{matrix} 2 y - a' tg φ = \frac{q sin φ}{1 + cos φ} (2 x - a - a'), \end{matrix}

tehát egyenes egyenlete.^{$^{*}$}
Ezen egyenes általában nem megy keresztül az origon, az

e

és

e'

egyenes metszőpontján.

x = 0

y = 0

csak akkor pontja az egyenesnek, ha

\begin{matrix} - a' tg φ = - \frac{q sin φ}{1 + q cos φ} (a + a'), vagyis a' (1 + q cos φ) = (a + a') q cos φ \end{matrix}

tehát, ha

\begin{matrix} \frac{a'}{cos φ} = q a . \end{matrix}

Azonban

\frac{a'}{cos φ} = O A'

a = O A

, azaz

O A' = q O A = \frac{O A}{k}

,
ill.

\begin{matrix} \frac{O A}{O A'} = k . \end{matrix}

Ez megegyezik azzal, amit az I. megoldáshoz fűzött jegyzetünkben fejeztünk ki.

^{$^{*}$}

\frac{1}{k} = q

helyettesítés tört kikerülése céljából. Éppen így írhattuk volna:

A' M' = k \cdot A M

^{$^{*}$}Ha $x = \frac{a + a'}{2}$ , akkor $y = \frac{a' tg φ}{2}$ . Az egyenes keresztülmegy $A A'$ felező pontján.