Kezdőlap


Feladat:	1336. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Czinczenheim József , Krisztonosich Jenő , Nagy Elemér , Schreiber Béla
Füzet:	1937/október, 50 - 51. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Egyenlő szárú háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek nevezetes tételei, Síkgeometriai bizonyítások, Feladat, Párhuzamos szelők tétele és megfordítása
Hivatkozás(ok):	Feladatok: 1937/május: 1336. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Stewart-tételével (l. Xlll. évf. 193. o. ─ azaz 1937/3 193. old. )

\begin{matrix} {\bar{C E}}^{2} \cdot c = a^{2} \cdot \bar{A E} + b^{2} \cdot \bar{E B} - \bar{A E} \cdot \bar{E B} \cdot c \\ {\bar{C E}}^{2} = a^{2} \cdot \frac{A E}{c} + b^{2} \frac{E B}{c} - \bar{A E} \cdot \bar{E B} ... & (1) \end{matrix}

ahol

c = A B

. Feltevésünk szerint

\begin{matrix} A E : c = n : (m + n) és E B : c = m : (m + n) . \end{matrix}

Tekintettel ezekre, 1)-ből keletkezik:

\begin{matrix} {\bar{C E}}^{2} = \frac{n a^{2}}{m + n} + \frac{m b^{2}}{m + n} - \frac{m n c^{2}}{{(m + n)}^{2}} = \frac{(n a^{2} + m b^{2}) (m + n) - m n c^{2}}{{(m + n)}^{2}} = \\ = \frac{n^{2} a^{2} + m^{2} b^{2} + m n (a^{2} + b^{2} - c^{2})}{{(m + n)}^{2}} = \frac{{(n a + m b)}^{2} + m n (a^{2} - 2 a b + b^{2} - c^{2})}{{(m + n)}^{2}} = \\ = {(\frac{n a + m b}{m + n})}^{2} - \frac{m n}{{(m + n)}^{2}} [c^{2} - {(a - b)}^{2}] . \end{matrix}

Minthogy

a

b

c

egy háromszög oldalai,

c^{2} > {(a - b)}^{2}

, úgy hogy

\begin{matrix} \frac{m n}{{(m + n)}^{2}} [c^{2} - {(a - b)}^{2}] > 0 \end{matrix}

tehát

{\bar{C E}}^{2} < {(\frac{n a + m b}{m + n})}^{2} azaz C E < \frac{n a + m b}{m + n}

.

Czinczenheim József (Izr. g. VIII. o. Debreeen).

II. Megoldás. Húzzunk az

A

és

B

pontokon keresztül

C E

-vel párhuzamosakat, ábránk szerint; az előbbire mérjük fel

A C_{1} = A C = b

, az utóbbira

B C_{2} = B C = a

távolságokat. Legyen már most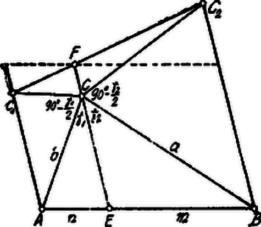

A C E ∢ = γ_{1}

B C E ∢ = γ_{2}

(γ_{1} + γ_{2} = γ)

Minthogy

A C_{1} ∥ C E

, a

C A C_{1}

egyenlőszárú háromszögben

C A C_{1} ∢ = γ_{1}

; a

C B C_{2} Δ

-ben

C B C_{2} ∢ = γ_{2}

. Ebből következik, hogy

\begin{matrix} A C C_{1} ∢ = 90^{\circ} - \frac{γ_{1}}{2}, B C C_{2} ∢ = 90^{\circ} - \frac{γ_{2}}{2} . \end{matrix}

C C_{1}

-t a

C

körül pozitív irányban forgatjuk, míg a

C C_{2}

helyzetbe kerül, a forgást domború szög méri, t. i.

\begin{matrix} C_{1} C A ∢ + A C B ∢ + B C C_{2} ∢ = \\ = 90^{\circ} - \frac{γ_{1}}{2} + γ + 90^{\circ} - \frac{γ_{2}}{2} = \\ = 180^{\circ} + γ - \frac{γ_{1} + γ_{2}}{2} = 180^{\circ} + \frac{γ}{2} . \end{matrix}

Ebből következik, hogy az

A B C_{2} C C_{1}

konkáv ötszög

C_{1} C_{2}

átlója az ötszöget nem hasítja, ill. a

C

pont az

A B C_{2} C_{1}

trapézen belül fekszik.
Hosszabbítsuk meg

C E

-t amíg

C_{1} C_{2}

-t az

F

pontban metszi, tehát

F E > C E

. A párhuzamos szelők törvényéből folyik, hogy

\begin{matrix} \frac{a - F E}{F E - b} és innen F E = \frac{n a + m b}{m + n} > C E . \end{matrix}

W. M.