Kezdőlap


Feladat:	1335. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Czinczenheim József , Komlós János
Füzet:	1937/október, 49 - 50. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Körérintők, Paraméteres egyenletek, Trapézok, Négyszögek középvonalai, Síkgeometriai számítások trigonometria nélkül körökben, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1937/május: 1335. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . Az adott körök középpontja $O_{1}$ , ill. $O_{2}$ , sugaruk $r_{1}$ ill. $r_{2}$ ; a külső érintők érintési pontjai $A_{1}$ , $A_{2}$ , ill. $B_{1}$ , $B_{2}$ , a belsőké $C_{1}$ , $C_{2}$ ill. $D_{1}$ , $D_{2}$ ; a metszéspontok az $A_{1} A_{2}$ érintőn $E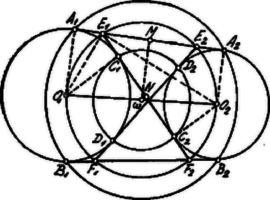_{1}$ , $E_{2}$ , a $B_{1} B_{2}$ érintőn $F_{1}$ és $F_{2}$ .

E_{1}

pontból az

O_{1}

körhöz húzott érintők ‐

E_{1} A_{1}

és

E_{1} C_{1}

‐ szögét felezi

E_{1} O_{1}

; hasonlóan

E_{1} O_{2}

felezi az

O_{2}

körhöz húzott érintők ‐ az

E_{1} A_{2}

és

E_{1} C_{2}

‐ szögét. A két szög egymásnak mellékszöge; tehát felezőik egymásra merőlegesek. Ebből következik, hogy

E_{1}

O_{1} O_{2}

átmérő fölé írt körön fekszik. Hasonló oknál fogva az

E_{2}

F_{1}

F_{2}

pontok is ugyanezen körön feküsznek. Ezen kör középpontja

ω

, az

O_{1} O_{2} = 2 a

centrális távolság felezőpontja; sugara

ϱ = a

2^{0}

A_{1} O_{1} ⊥ A_{1} A_{2}

és

A_{2} O_{2} ⊥ A_{1} A_{2}

. Ha tehát

A_{1} A_{2}

felezőpontjában,

M

-ben

A_{1} A_{2}

-re merőlegest emelünk, ez az

O_{1} O_{2}

felezőpontján megy keresztül, azaz

A_{1} A_{2}

oly kör húrja, melynek középpontja

ω

. Ugyanezen körön feküsznek

B_{1}

és

B_{2}

is, minthogy

B_{1}

A_{1}

B_{2}

A_{2}

szimmetrikus pontja az

O_{1} O_{2}

-re nézve.

Ismeretes, hogy

\begin{matrix} {\bar{A_{1} A_{2}}}^{2} = {(2 a)}^{2} - {(r_{1} - r_{2})}^{2} \end{matrix}

tehát

\begin{matrix} A_{1} M^{2} - {(\frac{A_{1} A_{2}}{2})}^{2} = a^{2} - {(\frac{r_{1} r_{2}}{2})}^{2} . \end{matrix}

M ω

A_{1} O_{1} O_{2} A_{2}

trapéz középvonala:

M ω = \frac{r_{1} + r_{2}}{2}

.
A külső érintők érintési pontjai köré irható kör sugara

ω A_{1} = ϱ_{1}

és

\begin{matrix} ϱ_{1}^{2} = {\bar{A_{1} M}}^{2} + {\bar{M ω}}^{2} = a^{2} - {(\frac{r_{1} - r_{2}}{2})}^{2} + {(\frac{r_{1} + r_{2}}{2})}^{2} = a^{2} + r_{1} r_{2} . \end{matrix}

3^{0}

ω

pontból a

C_{1} C_{2}

belső érintőre bocsátott merőleges,

ω N

párhuzamos az

O_{1} C_{1}

és

O_{2} C_{2}

sugarakkal; amint

ω

O_{1} O_{2}

-t, úgy

N

a

C_{1} C_{2}

-t felezi. Tehát

C_{1} C_{2}

egy, az

ω

körül írt kör húrja. Ugyanezen körön feküsznek

D_{1}

és

D_{2}

is, a

C_{1}

és

C_{2}

szimmetrikus pontjai az

ω

-n átmenő

O_{1} O_{2}

egyenesre nézve. Ezen kör és sugarának kiszámításánál vegyük figyelembe, hogy

\begin{matrix} {\bar{C_{1} C_{2}}}^{2} = {(2 a)}^{2} - {(r_{1} + r_{2})}^{2} és {\bar{C_{1} N}}^{2} = {(\frac{C_{1} C_{2}}{2})}^{2} = a^{2} - {(\frac{r_{1} + r_{2}}{2})}^{2} . \end{matrix}

Mivel

N ω = | \frac{r_{1} + r_{2}}{2} |

, azért

\begin{matrix} ϱ_{2}^{2} = {\bar{C_{1} N}}^{2} + {\bar{N ω}}^{2} = a^{2} - {(\frac{r_{1} + r_{2}}{2})}^{2} + 2 {(\frac{r_{1} - r_{2}}{2})}^{2} = a^{2} - r_{1} r_{2} . \end{matrix}

A szóbanforgó három koncentrikus kör sugara

\begin{matrix} ϱ = a, ϱ_{1} = a^{2} + r_{1} r_{2}, ϱ_{2} = a^{2} - r_{1} r_{2} . \end{matrix}

Komlós János (Gr. Széchenyi István g. VII. o. Pécs.)

Jegyzet. Az előbbi eredményből kitűnik, hogy

\begin{matrix} ϱ = \sqrt[]{\frac{ϱ_{1}^{2} + ϱ_{2}^{2}}{2}} \end{matrix}